Experiment 4A
Famous vs. non-famous faces (between-participants design)
Hongmi Lee, Kyungmi Kim, Do-Joon Yi
2019-04-02
set.seed(12345) # for reproducibility
options(knitr.kable.NA = '')
# Some packages need to be loaded. We use `pacman` as a package manager, which takes care of the other packages.
if (!require("pacman", quietly = TRUE)) install.packages("pacman")
if (!require("Rmisc", quietly = TRUE)) install.packages("Rmisc") # Never load it directly.
pacman::p_load(tidyverse, knitr, car, afex, emmeans, parallel, ordinal,
ggbeeswarm, RVAideMemoire)
pacman::p_load_gh("thomasp85/patchwork", "RLesur/klippy")
klippy::klippy()1 Item Repetition Phase
Forty eight participants were recruited.1 Half of the participants were exposed to 24 famous faces while the other half were exposed to 24 non-famous faces (pre-experimental stimulus familiarity as a between-participants factor). Each face was repeated eight times, resulting in 192 trials in total. Participants made a male/female judgment for each face.
P1 <- read.csv("data/data_FamSM_Exp4A_Face_REP.csv", header = T)
P1$Familiarity = factor(P1$Familiarity, levels=c(1,2), labels=c("Famous","Non-famous"))
glimpse(P1, width=70)
## Observations: 9,216
## Variables: 9
## $ SID <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ Familiarity <fct> Non-famous, Non-famous, Non-famous, Non-famous,…
## $ RepTime <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ Trial <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …
## $ ImgCat <int> 2, 1, 2, 1, 1, 2, 2, 2, 1, 2, 2, 1, 2, 1, 1, 1,…
## $ Resp <int> 2, 1, 2, 1, 1, 2, 2, 1, 1, 2, 2, 1, 2, 1, 1, 1,…
## $ Corr <int> 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ RT <dbl> 609.87, 585.12, 481.17, 537.09, 521.08, 833.08,…
## $ ImgName <fct> unknown_female06.jpg, unknown_male12.jpg, unkno…
# 1. SID: participant ID
# 2. Familiarity: pre-experimental familiarity. 1 = famous, 2 = non-famous
# 3. RepTime: number of repetitions, 1~8
# 4. Trial: 1~24
# 5. ImgCat: stimulus category. male vs. female
# 6. Resp: male/female judgment, 1 = male, 2 = female, 0 = no response
# 7. Corr: correctness, 1=correct, 0 = incorrect or no response
# 8. RT: reaction times in ms.
# 9. ImgName: name of stimuli
table(P1$Familiarity, P1$SID)
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
## Famous 0 192 0 192 0 192 0 192 0 192 0 192 0 192 0
## Non-famous 192 0 192 0 192 0 192 0 192 0 192 0 192 0 192
##
## 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
## Famous 192 0 192 0 192 0 192 0 192 0 192 0 192 0 192
## Non-famous 0 192 0 192 0 192 0 192 0 192 0 192 0 192 0
##
## 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
## Famous 0 192 0 192 0 192 0 192 0 192 0 192 0 192 0
## Non-famous 192 0 192 0 192 0 192 0 192 0 192 0 192 0 192
##
## 46 47 48
## Famous 192 0 192
## Non-famous 0 192 01.1 Accuracy
We calculated the mean and s.d. of individual participants’ mean percentage accuracy. Overall accuracy of the male/female judgment was high. The famous condition showed lower mean accuracy and larger variance than the non-famous condition. In the following plot, red points and error bars represent the means and 95% CIs (error bars are hidden behind the points).
# phase 1, subject-level, long-format
P1slong <- P1 %>% group_by(SID, Familiarity) %>%
summarise(Accuracy = mean(Corr)*100) %>%
ungroup()
# summary table
P1slong %>% group_by(Familiarity) %>%
summarise(M = mean(Accuracy), SD = sd(Accuracy)) %>%
ungroup() %>%
kable()| Familiarity | M | SD |
|---|---|---|
| Famous | 97.80816 | 3.1286933 |
| Non-famous | 98.78472 | 0.8911482 |
# group level, needed for printing & geom_pointrange
# Rmisc must be called indirectly due to incompatibility between plyr and dplyr.
P1g <- Rmisc::summarySE(data = P1slong, measurevar = "Accuracy", groupvars = "Familiarity")
ggplot(P1slong, aes(x=Familiarity, y=Accuracy)) +
geom_violin(width = 0.5, trim=TRUE) +
ggbeeswarm::geom_quasirandom(color = "blue", size = 3, alpha = 0.2, width = 0.2) +
geom_pointrange(P1g, inherit.aes=FALSE,
mapping=aes(x = Familiarity, y=Accuracy,
ymin = Accuracy - ci, ymax = Accuracy + ci),
colour="darkred", size = 1)+
coord_cartesian(ylim = c(50, 100), clip = "on") +
labs(x = "Pre-experimental Stimulus Familiarity",
y = "Male/Female Judgment \n Accuracy (%)") +
theme_bw(base_size = 18)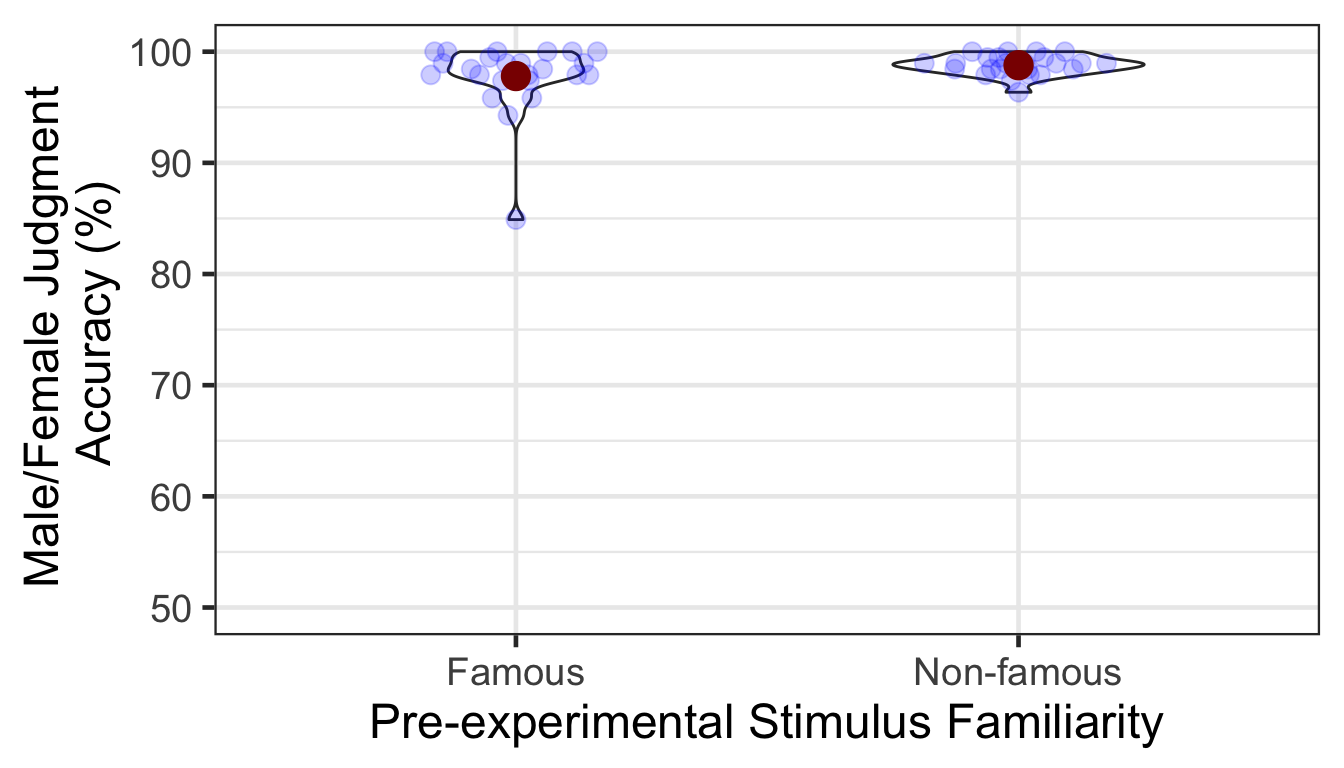
1.1.1 ANOVA
A one-way ANOVA showed that the accuracy was not significantly different between famous vs. non-famous conditions.
p1.aov <- aov_ez(id = "SID", dv = "Accuracy", data = P1slong, between = "Familiarity")
anova(p1.aov, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Familiarity | 1 | 46 | 5.2914 | 2.1628 | 0.0449 | 0.1482 |
2 Item-Source Association Phase
Participants learned 48 face-location (a quadrant on the screen) associations. They were instructed to pay attention to the location of each face while reporting in which quadrant a face appeared. A between-participants pre-experimental stimulus familiarity factor determined whether a participant viewed famous or non-famous faces. A within-participant item repetition factor determined whether a repeated item (which had been presented in the first phase) or an unrepeated item (which appeared for the first time in the item-source association phase) was presened in each trial.
P2 <- read.csv("data/data_FamSM_Exp4A_Face_SRC.csv", header = T)
P2$Familiarity = factor(P2$Familiarity, levels=c(1,2), labels=c("Famous","Non-famous"))
P2$Repetition = factor(P2$Repetition, levels=c(1,2), labels=c("Repeated","Unrepeated"))
glimpse(P2, width=70)
## Observations: 2,304
## Variables: 10
## $ SID <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ Familiarity <fct> Non-famous, Non-famous, Non-famous, Non-famous,…
## $ Trial <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …
## $ Repetition <fct> Repeated, Unrepeated, Repeated, Repeated, Unrep…
## $ ImgCat <int> 2, 1, 1, 1, 1, 2, 2, 1, 1, 2, 1, 2, 1, 1, 1, 2,…
## $ Loc <int> 4, 4, 1, 1, 4, 4, 2, 1, 4, 1, 3, 2, 3, 2, 4, 4,…
## $ Resp <int> 4, 4, 1, 1, 4, 4, 2, 1, 4, 1, 3, 2, 3, 2, 4, 4,…
## $ Corr <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ RT <dbl> 1127.69, 867.79, 879.91, 540.00, 840.05, 644.18…
## $ ImgName <fct> unknown_female21.jpg, unknown_male18.jpg, unkno…
# 1. SID: participant ID
# 2. Familiarity: pre-experimental familiarity. 1 = famous, 2 = non-famous
# 3. Trial: 1~48
# 4. Repetition: 1 = repeated, 2 = unrepeated
# 5. ImgCat: stimulus category. male vs. female
# 6. Loc: location (source) of memory item; quadrants, 1~4
# 7. Resp: male/female judgment, 1 = male, 2 = female, 0 = no response
# 8. Corr: correctness, 1 = correct, 0 = incorrect or no response
# 9. RT: reaction times in ms.
# 10. ImgName: name of stimuli
table(P2$Familiarity, P2$SID)
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## Famous 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48
## Non-famous 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0
##
## 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
## Famous 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48
## Non-famous 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0
##
## 41 42 43 44 45 46 47 48
## Famous 0 48 0 48 0 48 0 48
## Non-famous 48 0 48 0 48 0 48 0
table(P2$Repetition, P2$SID)
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## Repeated 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24
## Unrepeated 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24
##
## 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
## Repeated 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24
## Unrepeated 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24
##
## 41 42 43 44 45 46 47 48
## Repeated 24 24 24 24 24 24 24 24
## Unrepeated 24 24 24 24 24 24 24 242.1 Accuracy
We calculated the mean and s.d. of individual participants’ mean percentage accuracy. The overall performance was at ceiling.
# phase 2, subject-level, long-format
P2slong <- P2 %>% group_by(SID, Familiarity, Repetition) %>%
summarise(Accuracy = mean(Corr)*100) %>%
ungroup()
# summary table
P2g <- P2slong %>% group_by(Familiarity, Repetition) %>%
summarise(M = mean(Accuracy), SD = sd(Accuracy)) %>%
ungroup()
P2g %>% kable()| Familiarity | Repetition | M | SD |
|---|---|---|---|
| Famous | Repeated | 99.65278 | 1.1763744 |
| Famous | Unrepeated | 99.13194 | 2.1207391 |
| Non-famous | Repeated | 99.65278 | 1.1763744 |
| Non-famous | Unrepeated | 99.82639 | 0.8505173 |
# group level, needed for printing & geom_pointrange
# Rmisc must be called indirectly due to incompatibility between plyr and dplyr.
P2g$ci <- Rmisc::summarySEwithin(data = P2slong, measurevar = "Accuracy", idvar = "SID",
withinvars = "Repetition", betweenvars = "Familiarity")$ci
P2g$Accuracy <- P2g$M
ggplot(data=P2slong, aes(x=Familiarity, y=Accuracy, fill=Repetition)) +
geom_violin(width = 0.7, trim=TRUE) +
ggbeeswarm::geom_quasirandom(dodge.width = 0.7, color = "blue", size = 3, alpha = 0.2,
show.legend = FALSE) +
# geom_pointrange(data=P2g,
# aes(x = Familiarity, ymin = Accuracy-ci, ymax = Accuracy+ci, color = Repetition),
# position = position_dodge(0.7), color = "darkred", size = 1, show.legend = FALSE) +
coord_cartesian(ylim = c(50, 100), clip = "on") +
labs(x = "Pre-experimental Stimulus Familiarity",
y = "Localization Accuracy (%)",
fill='Item Repetition') +
scale_fill_manual(values=c("#E69F00", "#56B4E9"),
labels=c("Repeated", "Unrepeated")) +
theme_bw(base_size = 18) +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank()) 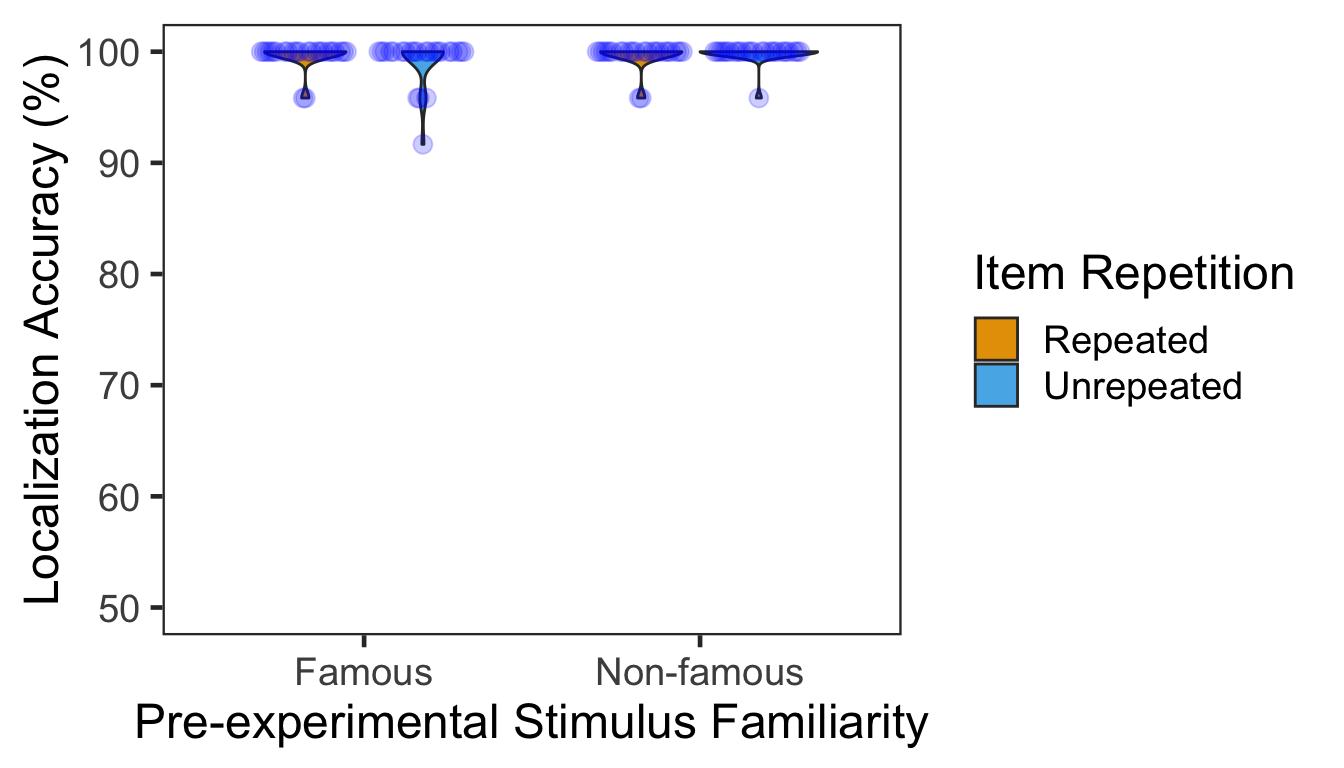
2.1.1 ANOVA
Mean percentage accuracy was submitted to a 2x2 mixed design ANOVA with pre-experimental stimulus familiarity as a between-participants factor and item repetition as a within-participant factor. No effects were significant.
p2.aov <- aov_ez(id = "SID", dv = "Accuracy", data = P2slong,
between = "Familiarity", within = "Repetition")
anova(p2.aov, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Familiarity | 1 | 46 | 1.8084 | 1.6000 | 0.0336 | 0.2123 |
| Repetition | 1 | 46 | 2.1859 | 0.3309 | 0.0071 | 0.5679 |
| Familiarity:Repetition | 1 | 46 | 2.1859 | 1.3237 | 0.0280 | 0.2559 |
3 Source Memory Test Phase
In each trial, participants first indicated in which quadrant a given face appeared during the item-source association phase. Participants then rated how confident they were about their memory judgment. There were 48 trials in total. pre-experimental stimulus familiarity was a between-participants factor. Item repetition was a within-participant factor.
P3 <- read.csv("data/data_FamSM_Exp4A_Face_TST.csv", header = T)
P3$Familiarity = factor(P3$Familiarity, levels=c(1,2), labels=c("Famous","Non-famous"))
P3$Repetition = factor(P3$Repetition, levels=c(1,2), labels=c("Repeated","Unrepeated"))
glimpse(P3, width=70)
## Observations: 2,304
## Variables: 10
## $ SID <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ Familiarity <fct> Non-famous, Non-famous, Non-famous, Non-famous,…
## $ Trial <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …
## $ Repetition <fct> Unrepeated, Unrepeated, Repeated, Unrepeated, U…
## $ AscLoc <int> 2, 4, 2, 1, 2, 1, 4, 4, 2, 1, 3, 4, 1, 2, 2, 4,…
## $ SrcResp <int> 1, 1, 2, 2, 2, 1, 3, 1, 2, 1, 3, 3, 1, 1, 2, 1,…
## $ Corr <int> 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0,…
## $ RT <dbl> 6357.03, 5074.45, 2951.22, 1915.16, 1394.97, 48…
## $ Confident <int> 1, 1, 1, 4, 4, 1, 4, 1, 4, 4, 1, 3, 1, 1, 4, 1,…
## $ ImgName <fct> unknown_female03.jpg, unknown_male18.jpg, unkno…
# 1. SID: participant ID
# 2. Familiarity: pre-experimental familiarity. 1 = famous, 2 = non-famous
# 3. Trial: 1~48
# 4. Repetition: 1 = repeated, 2 = unrepeated
# 5. AscLoc: location (source) in which the item was presented in Phase 2; quadrants, 1~4
# 6. SrcResp: source response; quadrants, 1~4
# 7. Corr: correctness, 1=correct, 0=incorrect
# 8. RT: reaction times in ms.
# 9. Confident: confidence rating, 1~4
# 10. ImgName: name of stimuli
table(P3$Familiarity, P3$SID)
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## Famous 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48
## Non-famous 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0
##
## 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
## Famous 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48
## Non-famous 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0 48 0
##
## 41 42 43 44 45 46 47 48
## Famous 0 48 0 48 0 48 0 48
## Non-famous 48 0 48 0 48 0 48 0
table(P3$Repetition, P3$SID)
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## Repeated 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24
## Unrepeated 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24
##
## 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
## Repeated 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24
## Unrepeated 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24 24
##
## 41 42 43 44 45 46 47 48
## Repeated 24 24 24 24 24 24 24 24
## Unrepeated 24 24 24 24 24 24 24 243.1 Accuracy
We calculated the mean and s.d. of individual participants’ mean percentage accuracy. In the following plot, red points and error bars represent the means and 95% within-participants CIs.
# phase 3, subject-level, long-format
P3ACCslong <- P3 %>% group_by(SID, Familiarity, Repetition) %>%
summarise(Accuracy = mean(Corr)*100) %>%
ungroup()
# summary table
P3ACCg <- P3ACCslong %>% group_by(Familiarity, Repetition) %>%
summarise(M = mean(Accuracy), SD = sd(Accuracy)) %>%
ungroup()
P3ACCg %>% kable()| Familiarity | Repetition | M | SD |
|---|---|---|---|
| Famous | Repeated | 56.59722 | 19.77060 |
| Famous | Unrepeated | 70.13889 | 17.57775 |
| Non-famous | Repeated | 57.46528 | 14.99694 |
| Non-famous | Unrepeated | 45.65972 | 14.45879 |
# marginal means of famous vs. non-famous conditions.
P3ACCslong %>% group_by(Familiarity) %>%
summarise(M = mean(Accuracy), SD = sd(Accuracy)) %>%
ungroup() %>% kable()| Familiarity | M | SD |
|---|---|---|
| Famous | 63.36806 | 19.73072 |
| Non-famous | 51.56250 | 15.74643 |
# marginal means of repeated vs. unrepeated conditions.
P3ACCslong %>% group_by(Repetition) %>%
summarise(M = mean(Accuracy), SD = sd(Accuracy)) %>%
ungroup() %>% kable()| Repetition | M | SD |
|---|---|---|
| Repeated | 57.03125 | 17.36473 |
| Unrepeated | 57.89931 | 20.16187 |
# wide format, needed for geom_segments.
P3ACCswide <- P3ACCslong %>% spread(key = Repetition, value = Accuracy)
# group level, needed for printing & geom_pointrange
# Rmisc must be called indirectly due to incompatibility between plyr and dplyr.
P3ACCg$ci <- Rmisc::summarySEwithin(data = P3ACCslong, measurevar = "Accuracy", idvar = "SID",
withinvars = "Repetition", betweenvars = "Familiarity")$ci
P3ACCg$Accuracy <- P3ACCg$M
ggplot(data=P3ACCslong, aes(x=Familiarity, y=Accuracy, fill=Repetition)) +
geom_violin(width = 0.5, trim=TRUE) +
geom_point(position=position_dodge(0.5), color="gray80", size=1.8, show.legend = FALSE) +
geom_segment(data=filter(P3ACCswide, Familiarity=="Famous"), inherit.aes = FALSE,
aes(x=1-.12, y=filter(P3ACCswide, Familiarity=="Famous")$Repeated,
xend=1+.12, yend=filter(P3ACCswide, Familiarity=="Famous")$Unrepeated),
color="gray80") +
geom_segment(data=filter(P3ACCswide, Familiarity=="Non-famous"), inherit.aes = FALSE,
aes(x=2-.12, y=filter(P3ACCswide, Familiarity=="Non-famous")$Repeated,
xend=2+.12, yend=filter(P3ACCswide, Familiarity=="Non-famous")$Unrepeated),
color="gray80") +
geom_pointrange(data=P3ACCg,
aes(x = Familiarity, ymin = Accuracy-ci, ymax = Accuracy+ci, group = Repetition),
position = position_dodge(0.5), color = "darkred", size = 1, show.legend = FALSE) +
scale_fill_manual(values=c("#E69F00", "#56B4E9"),
labels=c("Repeated", "Unrepeated")) +
labs(x = "Pre-experimental Stimulus Familiarity",
y = "Source Memory Accuracy (%)",
fill='Item Repetition') +
coord_cartesian(ylim = c(0, 100), clip = "on") +
theme_bw(base_size = 18) +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank()) 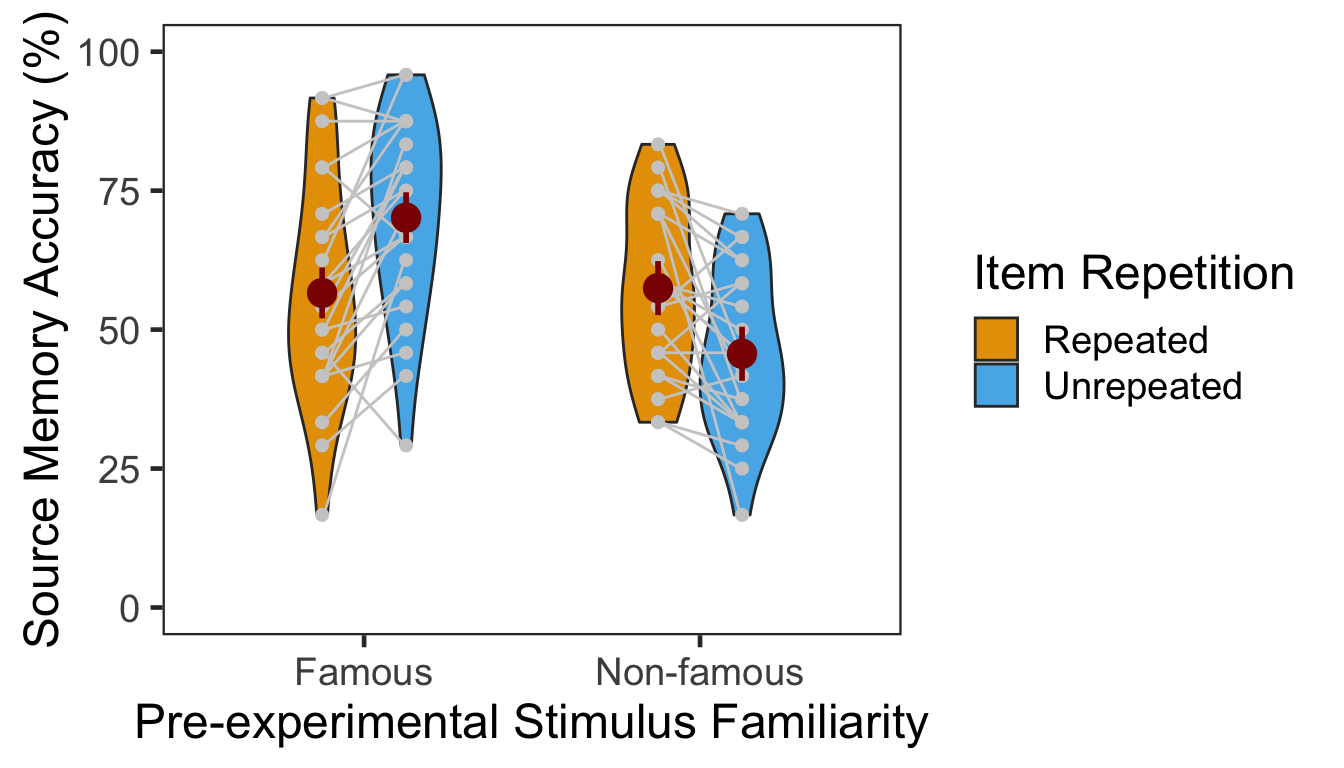
The effect of item repetition was modulated by the pre-experimental stimulus familiarity of the items. For famous faces, the locations of unrepeated items were better remembered (novelty benefit). For non-famous faces, the locations of repeated items were better remembered (familiarity benefit). These crossed effects were on top of the general familiarity benefit, in which source memory was more accurate for famous faces than for non-famous faces.
3.1.1 ANOVA
Individuals’ mean percentage accuracy was submitted to a 2x2 mixed design ANOVA with pre-experimental stimulus familiarity as a between-participants factor (famous vs. non-famous) and item repetition as a within-participant factor (Repeated vs. Unrepeated).
p3.corr.aov <- aov_ez(id = "SID", dv = "Accuracy", data = P3ACCslong,
between = "Familiarity", within = "Repetition")
anova(p3.corr.aov, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Familiarity | 1 | 46 | 442.0164 | 7.5674 | 0.1413 | 0.0085 |
| Repetition | 1 | 46 | 124.8931 | 0.1448 | 0.0031 | 0.7053 |
| Familiarity:Repetition | 1 | 46 | 124.8931 | 30.8655 | 0.4016 | 0.0000 |
The main effect of pre-experimental stimulus familiarity and the two-way interaction were both significant. Additionally, we performed two separate one-way repeated-measures ANOVAs as post-hoc analyses. The table below shows the effect of item repetition for famous faces.
ci95 <- P3ACCswide %>% filter(Familiarity=="Famous") %>%
mutate(Diff = Unrepeated - Repeated) %>%
summarise(lower = mean(Diff) - qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()),
upper = mean(Diff) + qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()))
p3.corr.aov.r1 <- aov_ez(id = "SID", dv = "Accuracy", within = "Repetition",
data = filter(P3ACCslong, Familiarity == "Famous"))
anova(p3.corr.aov.r1, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 23 | 117.1875 | 18.7778 | 0.4495 | 2e-04 |
In the famous face group, source memory was more accurate for unrepeated than repeated faces. The 95% CI of difference between the means was [7.08, 20.01]. The table below shows the effect of item repetition for non-famous faces.
ci95 <- P3ACCswide %>% filter(Familiarity=="Non-famous") %>%
mutate(Diff = Repeated - Unrepeated) %>%
summarise(lower = mean(Diff) - qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()),
upper = mean(Diff) + qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()))
p3.corr.aov.r2 <- aov_ez(id = "SID", dv = "Accuracy", within = "Repetition",
data = filter(P3ACCslong, Familiarity == "Non-famous"))
anova(p3.corr.aov.r2, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 23 | 132.5986 | 12.6129 | 0.3542 | 0.0017 |
In the non-famous face group, source memory was more accurate for repeated than unrepeated faces. The 95% CI of difference between the means was [4.93, 18.68].
3.1.2 GLMM
To supplement conventional ANOVAs, we tested GLMMs on source memory accuracy. This mixed modeling approach with a binomial link function is expected to properly handle binary data such as source memory responses (i.e., correct or not; Jaeger, 2008).
We built the full model (full1) with two fixed effects (pre-experimental stimulus familiarity and item repetition) and their interaction. The model also included maximal random effects structure (Barr, Levy, Scheepers, & Tily, 2013): both by-participant and by-item random intercepts, and by-participant random slopes for item repetition. In case the maximal model does not converge successfully, we built another model (full2) with the maximal random structure but with the correlations among the random terms removed (Singmann, 2018).
To fit the models, we used the mixed() of the afex package (Singmann, Bolker, & Westfall, 2017) which was built on the lmer() of the lme4 package (Bates, Maechler, Bolker, & Walker, 2015). The mixed() assessed the statistical significance of fixed effects by comparing a model with the effect in question against its nested model which lacked the effect in question. P-values of the effects were obtained by likelihood ratio tests (LRT).
(nc <- detectCores())
cl <- makeCluster(rep("localhost", nc))
full1 <- afex::mixed(Corr ~ Familiarity*Repetition + (Repetition|SID) + (1|ImgName),
P3, method = "LRT", cl = cl,
family=binomial(link="logit"),
control = glmerControl(optCtrl = list(maxfun = 1e6)))
full2 <- afex::mixed(Corr ~ Familiarity*Repetition + (Repetition||SID) + (1|ImgName),
P3, method = "LRT", cl = cl,
family=binomial(link="logit"),
control = glmerControl(optCtrl = list(maxfun = 1e6)), expand_re = TRUE)
stopCluster(cl)The table below presents the LRT results of the models full1 and full2.
full.compare <- cbind(afex::nice(full1), afex::nice(full2)[,-c(1,2)])
colnames(full.compare)[c(3,4,5,6)] <- c("full1 Chisq", "p", "full2 Chisq", "p")
full.compare %>% kable()| Effect | df | full1 Chisq | p | full2 Chisq | p |
|---|---|---|---|---|---|
| Familiarity | 1 | 7.22 ** | .007 | 7.25 ** | .007 |
| Repetition | 1 | 0.47 | .49 | 0.51 | .47 |
| Familiarity:Repetition | 1 | 25.11 *** | <.0001 | 25.53 *** | <.0001 |
The p-values from the two models were highly similar to each other. Post-hoc analysis results are summarized in the table below. The results from the pairwise comparisons were consistent with those from the ANOVA. Item repetition impaired source memory for famous faces whereas it improved source memory for non-famous faces.
emmeans(full1, pairwise ~ Repetition | Familiarity, type = "response")$contrasts %>% kable()| contrast | Familiarity | odds.ratio | SE | df | z.ratio | p.value |
|---|---|---|---|---|---|---|
| Repeated / Unrepeated | Famous | 0.5200752 | 0.0772337 | Inf | -4.402426 | 0.0000107 |
| Repeated / Unrepeated | Non-famous | 1.6703859 | 0.2330347 | Inf | 3.677560 | 0.0002355 |
3.2 Confidence
The table below presents the mean and s.d. of individual participants’ confidence ratings in each condition. The pattern of confidence ratings was qualitatively identical to that of source memory accuracy; we observed the novelty benefit for famous faces and the familiarity benefit for non-famous faces. In the following plot, red points and error bars represent the means and 95% within-participants CIs.
P3CFslong <- P3 %>% group_by(SID, Familiarity, Repetition) %>%
summarise(Confidence = mean(Confident)) %>%
ungroup()
P3CFg <- P3CFslong %>%
group_by(Familiarity, Repetition) %>%
summarise(M = mean(Confidence), SD = sd(Confidence)) %>%
ungroup()
P3CFg %>% kable()| Familiarity | Repetition | M | SD |
|---|---|---|---|
| Famous | Repeated | 2.689236 | 0.4577531 |
| Famous | Unrepeated | 2.942708 | 0.5883342 |
| Non-famous | Repeated | 2.807292 | 0.5439351 |
| Non-famous | Unrepeated | 2.133681 | 0.4987877 |
# marginal means of famous vs. non-famous conditions.
P3CFslong %>% group_by(Familiarity) %>%
summarise(M = mean(Confidence), SD = sd(Confidence)) %>%
ungroup() %>% kable()| Familiarity | M | SD |
|---|---|---|
| Famous | 2.815972 | 0.5369636 |
| Non-famous | 2.470486 | 0.6183726 |
# marginal means of repeated vs. unrepeated conditions.
P3CFslong %>% group_by(Repetition) %>%
summarise(M = mean(Confidence), SD = sd(Confidence)) %>%
ungroup() %>% kable()| Repetition | M | SD |
|---|---|---|
| Repeated | 2.748264 | 0.5008827 |
| Unrepeated | 2.538194 | 0.6769395 |
# wide format, needed for geom_segments.
P3CFswide <- P3CFslong %>% spread(key = Repetition, value = Confidence)
# group level, needed for printing & geom_pointrange
# Rmisc must be called indirectly due to incompatibility between plyr and dplyr.
P3CFg$ci <- Rmisc::summarySEwithin(data = P3CFslong, measurevar = "Confidence", idvar = "SID",
withinvars = "Repetition", betweenvars = "Familiarity")$ci
P3CFg$Confidence <- P3CFg$M
ggplot(data=P3CFslong, aes(x=Familiarity, y=Confidence, fill=Repetition)) +
geom_violin(width = 0.5, trim=TRUE) +
geom_point(position=position_dodge(0.5), color="gray80", size=1.8, show.legend = FALSE) +
geom_segment(data=filter(P3CFswide, Familiarity=="Famous"), inherit.aes = FALSE,
aes(x=1-.12, y=filter(P3CFswide, Familiarity=="Famous")$Repeated,
xend=1+.12, yend=filter(P3CFswide, Familiarity=="Famous")$Unrepeated),
color="gray80") +
geom_segment(data=filter(P3CFswide, Familiarity=="Non-famous"), inherit.aes = FALSE,
aes(x=2-.12, y=filter(P3CFswide, Familiarity=="Non-famous")$Repeated,
xend=2+.12, yend=filter(P3CFswide, Familiarity=="Non-famous")$Unrepeated),
color="gray80") +
geom_pointrange(data=P3CFg,
aes(x = Familiarity, ymin = Confidence-ci, ymax = Confidence+ci, group = Repetition),
position = position_dodge(0.5), color = "darkred", size = 1, show.legend = FALSE) +
scale_fill_manual(values=c("#E69F00", "#56B4E9"),
labels=c("Repeated", "Unrepeated")) +
labs(x = "Pre-experimental Stimulus Familiarity",
y = "Source Memory Confidence",
fill='Item Repetition') +
coord_cartesian(ylim = c(1, 4), clip = "on") +
theme_bw(base_size = 18) +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank())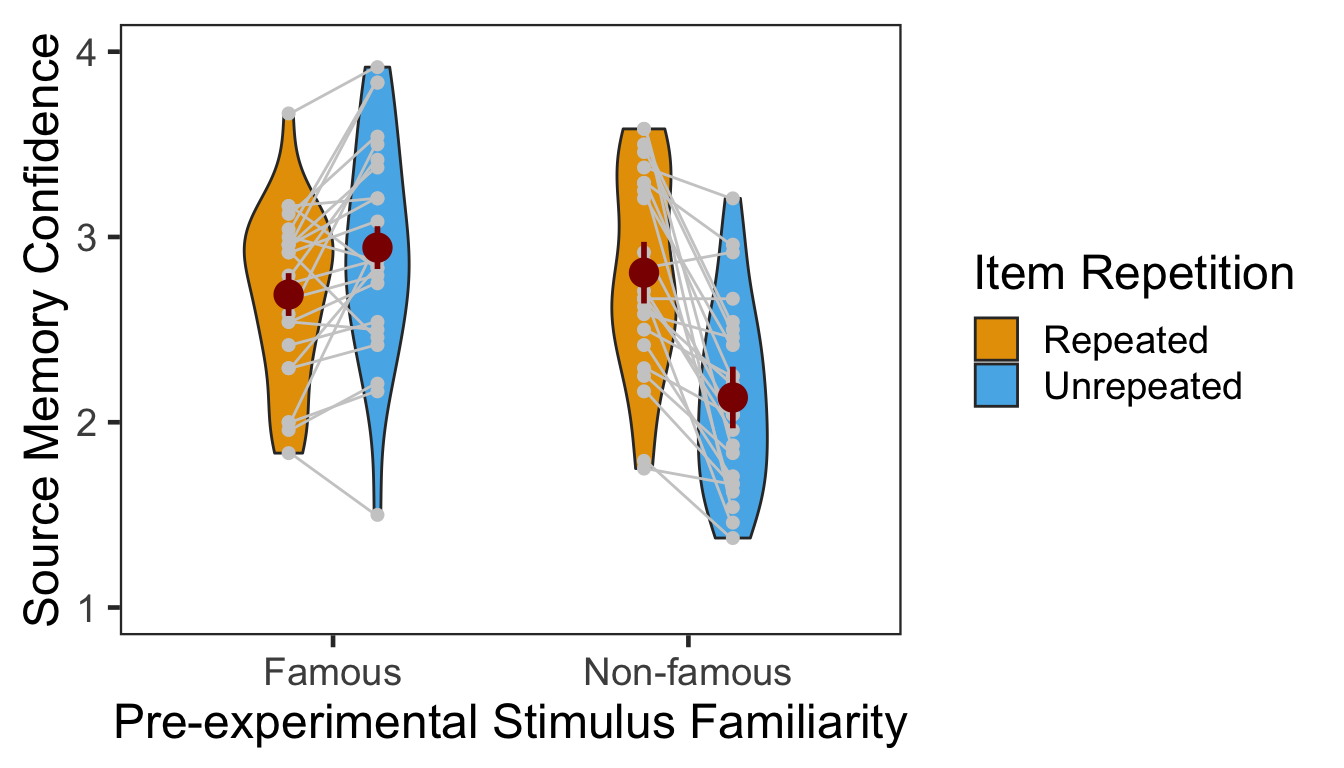
3.2.1 ANOVA
Individuals’ confidence ratings were submitted to a 2x2 mixed design ANOVA with pre-experimental stimulus familiarity as a between-participants factor and item repetition as a within-participant factor.
p3.conf.aov <- aov_ez(id = "SID", dv = "Confidence", data = P3CFslong,
between = "Familiarity", within = "Repetition")
anova(p3.conf.aov, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Familiarity | 1 | 46 | 0.4353 | 6.5815 | 0.1252 | 0.0136 |
| Repetition | 1 | 46 | 0.1149 | 9.2170 | 0.1669 | 0.0039 |
| Familiarity:Repetition | 1 | 46 | 0.1149 | 44.8788 | 0.4938 | 0.0000 |
The two-way interaction as well as both main effects reached significance. Next we performed two additional one-way repeated-measures ANOVAs as post-hoc analyses. The first table below presents the effect of item repetition for famous faces, and the second presents the same effect for non-famous faces.
ci95 <- P3CFswide %>% filter(Familiarity=="Famous") %>%
mutate(Diff = Unrepeated - Repeated) %>%
summarise(lower = mean(Diff) - qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()),
upper = mean(Diff) + qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()))
p3.conf.aov.r1 <- aov_ez(id = "SID", dv = "Confidence", within = "Repetition",
data = filter(P3CFslong, Familiarity == "Famous"))
anova(p3.conf.aov.r1, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 23 | 0.0748 | 10.3075 | 0.3095 | 0.0039 |
In the famous face group, confidence ratings were higher for unrepeated than repeated faces. The 95% CI of difference between the means was [0.09, 0.42].
ci95 <- P3CFswide %>% filter(Familiarity=="Non-famous") %>%
mutate(Diff = Repeated - Unrepeated) %>%
summarise(lower = mean(Diff) - qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()),
upper = mean(Diff) + qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()))
p3.conf.aov.r2 <- aov_ez(id = "SID", dv = "Confidence", within = "Repetition",
data = filter(P3CFslong, Familiarity == "Non-famous"))
anova(p3.conf.aov.r2, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 23 | 0.155 | 35.1253 | 0.6043 | 0 |
In the non-famous face group, confidence ratings were higher for repeated than unrepeated faces. The 95% CI of difference between the means was [0.44, 0.91].
3.2.2 CLMM
The responses from a Likert-type scale are ordinal. Especially for the rating items with numerical response formats containing four or fewer categories, it is recommended to use categorical data analysis approaches, rather than treating the responses as continuous data (Harpe, 2015).
Here we employed the cumulative link mixed modeling using the clmm() of the package ordinal (Christensen, submitted). The specification of the full model was the same as the mixed() above. To determine the statistical significance, the LRT compared models with or without the fixed effect of interest.
P3R <- P3
P3R$Confident = factor(P3R$Confident, ordered = TRUE)
P3R$SID = factor(P3R$SID)
cm.full <- clmm(Confident ~ Familiarity * Repetition + (Repetition|SID) + (1|ImgName), data=P3R)
cm.red1 <- clmm(Confident ~ Familiarity + Repetition + (Repetition|SID) + (1|ImgName), data=P3R)
cm.red2 <- clmm(Confident ~ Repetition + (Repetition|SID) + (1|ImgName), data=P3R)
cm.red3 <- clmm(Confident ~ 1 + (Repetition|SID) + (1|ImgName), data=P3R) cm.comp <- anova(cm.full, cm.red1, cm.red2, cm.red3)
data.frame(Effect = c("Familiarity", "Repetition", "Familiarity:Repetition"),
df = 1, Chisq = cm.comp$LR.stat[2:4], p = cm.comp$`Pr(>Chisq)`[2:4]) %>% kable()| Effect | df | Chisq | p |
|---|---|---|---|
| Familiarity | 1 | 3.4316676 | 0.0639575 |
| Repetition | 1 | 0.3860451 | 0.5343856 |
| Familiarity:Repetition | 1 | 32.7947040 | 0.0000000 |
The LRT revealed a significant two-way interaction. No main effects were significant. Next we performed pairwise comparisons as post-hoc analyses. As shown in the following table, the results of the pairwise comparisons were consistent with those from the ANOVA approach.
emmeans(cm.full, pairwise ~ Repetition | Familiarity)$contrasts %>% kable()| contrast | Familiarity | estimate | SE | df | z.ratio | p.value |
|---|---|---|---|---|---|---|
| Repeated - Unrepeated | Famous | -0.5496718 | 0.1881596 | Inf | -2.921305 | 0.0034857 |
| Repeated - Unrepeated | Non-famous | 1.2514894 | 0.1861433 | Inf | 6.723259 | 0.0000000 |
Below is the plot of estimated marginal means, which were extracted from the fitted CLMM. The estimated distribution of confidence ratings shows the interaction between item repetition and pre-experimental stimulus familiarity.
temp <- emmeans(cm.full,~Familiarity:Repetition|cut, mode="linear.predictor")
temp <- rating.emmeans(temp)
temp <- temp %>% unite(Condition, c("Familiarity", "Repetition"))
ggplot(data = temp, aes(x = Rating, y = Prob, group = Condition)) +
geom_line(aes(color = Condition), size = 1.2) +
geom_point(aes(shape = Condition, color = Condition), size = 4, fill = "white", stroke = 1.2) +
scale_color_manual(values=c("#E69F00", "#E69F00", "#56B4E9", "#56B4E9")) +
scale_shape_manual(name="Condition", values=c(21,24,21,24)) +
labs(y = "Response Probability", x = "Rating") +
expand_limits(y=0) +
scale_y_continuous(limits = c(0, 0.5)) +
scale_x_discrete(labels = c("1" = "1(Guessed)","4"="4(Sure)")) +
theme_minimal() +
theme(text = element_text(size=18))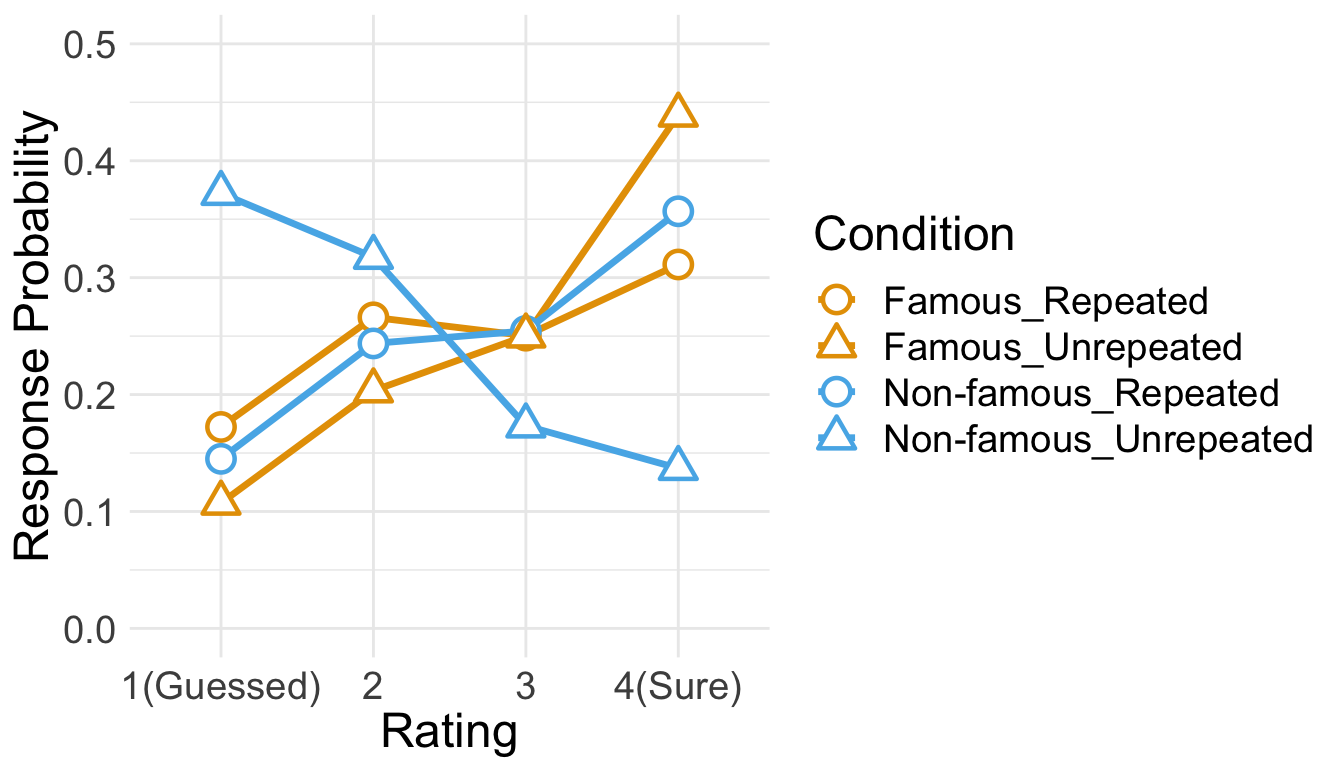
3.3 RT
Only RTs from correct trials were analyzed. Before analysis, we first removed RTs either shorter than 200ms or longer than 10s. Then, from the RT distribution of each participant, RTs beyond 3 s.d. from the mean were additionally removed.
cP3 <- P3 %>% filter(Corr==1)
sP3 <- cP3 %>% filter(RT > 200 & RT < 10000) %>%
group_by(SID) %>%
nest() %>%
mutate(lbound = map(data, ~mean(.$RT)-3*sd(.$RT)),
ubound = map(data, ~mean(.$RT)+3*sd(.$RT))) %>%
unnest(lbound, ubound) %>%
unnest(data) %>%
ungroup() %>%
mutate(Outlier = (RT < lbound)|(RT > ubound)) %>%
filter(Outlier == FALSE) %>%
select(SID, Familiarity, Repetition, RT, ImgName)
100 - 100*nrow(sP3)/nrow(cP3)
## [1] 5.362538This trimming procedure removed 5.36% of correct trials.
Since the overall source memory accuracy was not high, only small numbers of correct trials were available after trimming. The following table summarizes the numbers of RTs submitted to subsequent analyses. No participant had more than 25 trials per condition.
sP3 %>% group_by(SID, Familiarity, Repetition) %>%
summarise(NumTrial = length(RT)) %>%
ungroup() %>%
group_by(Familiarity, Repetition) %>%
summarise(Mean = mean(NumTrial),
Median = median(NumTrial),
Min = min(NumTrial),
Max = max(NumTrial)) %>%
ungroup %>%
kable()| Familiarity | Repetition | Mean | Median | Min | Max |
|---|---|---|---|---|---|
| Famous | Repeated | 12.83333 | 12.5 | 4 | 21 |
| Famous | Unrepeated | 16.37500 | 17.0 | 7 | 23 |
| Non-famous | Repeated | 12.95833 | 13.0 | 8 | 19 |
| Non-famous | Unrepeated | 10.04167 | 10.0 | 3 | 16 |
den1 <- ggplot(cP3, aes(x=RT)) +
geom_density() +
theme_bw(base_size = 18) +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank())
den2 <- ggplot(sP3, aes(x=RT)) +
geom_density() +
theme_bw(base_size = 18) +
labs(x = "Trimmed RT") +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank())
den1 + den2
The overall RT distribution was highly skewed even after trimming. Given limited numbers of RTs and its skewed distribution, any results from the current RT analyses should be interpreted with caution and preferably corroborated with other measures.
We calculated the mean and s.d. of individual participants’ mean RTs. The overall pattern of RTs across the conditions was consistent with that of source memory accuracy and confidence ratings. In the following plot, red points and error bars represent the means and 95% within-participants CIs.
P3RTslong <- sP3 %>% group_by(SID, Familiarity, Repetition) %>%
summarise(RT = mean(RT)) %>%
ungroup()
P3RTg <- P3RTslong %>% group_by(Familiarity, Repetition) %>%
summarise(M = mean(RT), SD = sd(RT)) %>%
ungroup()
P3RTg %>% kable()| Familiarity | Repetition | M | SD |
|---|---|---|---|
| Famous | Repeated | 2389.634 | 710.8305 |
| Famous | Unrepeated | 1943.214 | 670.0161 |
| Non-famous | Repeated | 2994.780 | 946.9946 |
| Non-famous | Unrepeated | 3177.818 | 927.3634 |
# wide format, needed for geom_segments.
P3RTswide <- P3RTslong %>% spread(key = Repetition, value = RT)
# group level, needed for printing & geom_pointrange
# Rmisc must be called indirectly due to incompatibility between plyr and dplyr.
P3RTg$ci <- Rmisc::summarySEwithin(data = P3RTslong, measurevar = "RT", idvar = "SID",
withinvars = "Repetition", betweenvars = "Familiarity")$ci
P3RTg$RT <- P3RTg$M
ggplot(data=P3RTslong, aes(x=Familiarity, y=RT, fill=Repetition)) +
geom_violin(width = 0.5, trim=TRUE) +
geom_point(position=position_dodge(0.5), color="gray80", size=1.8, show.legend = FALSE) +
geom_segment(data=filter(P3RTswide, Familiarity=="Famous"), inherit.aes = FALSE,
aes(x=1-.12, y=filter(P3RTswide, Familiarity=="Famous")$Repeated,
xend=1+.12, yend=filter(P3RTswide, Familiarity=="Famous")$Unrepeated),
color="gray80") +
geom_segment(data=filter(P3RTswide, Familiarity=="Non-famous"), inherit.aes = FALSE,
aes(x=2-.12, y=filter(P3RTswide, Familiarity=="Non-famous")$Repeated,
xend=2+.12, yend=filter(P3RTswide, Familiarity=="Non-famous")$Unrepeated),
color="gray80") +
geom_pointrange(data=P3RTg,
aes(x = Familiarity, ymin = RT-ci, ymax = RT+ci, group = Repetition),
position = position_dodge(0.5), color = "darkred", size = 1, show.legend = FALSE) +
scale_fill_manual(values=c("#E69F00", "#56B4E9"),
labels=c("Repeated", "Unrepeated")) +
labs(x = "Pre-experimental Stimulus Familiarity",
y = "Response Times (ms)",
fill='Item Repetition') +
theme_bw(base_size = 18) +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank())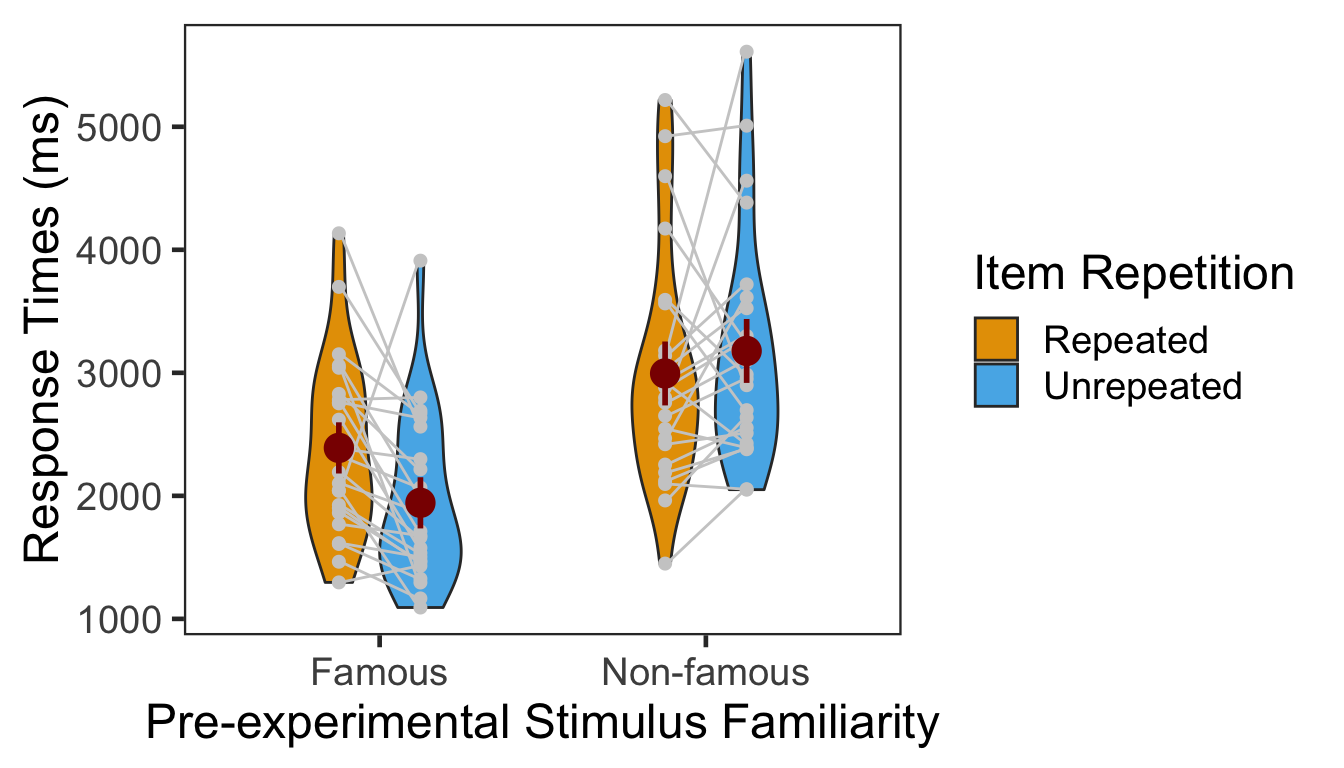
3.3.1 ANOVA
Individuals’ mean RTs were submitted to a 2x2 mixed design ANOVA with pre-experimental stimulus familiarity as a between-participants factor and item repetition as a within-participant factor.
p3.rt.aov <- aov_ez(id = "SID", dv = "RT", data = sP3,
between = "Familiarity", within = "Repetition")
anova(p3.rt.aov, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Familiarity | 1 | 46 | 1044889.5 | 19.4356 | 0.2970 | 0.0001 |
| Repetition | 1 | 46 | 310612.1 | 1.3400 | 0.0283 | 0.2530 |
| Familiarity:Repetition | 1 | 46 | 310612.1 | 7.6536 | 0.1426 | 0.0081 |
The main effect of pre-experimental stimulus familiarity and the two-way interaction were both significant. We then performed two one-way repeated-measures ANOVAs as post-hoc analyses. The first table below presents the effect of item repetition for famous faces, and the second table presents the same effect for non-famous faces.
p3.rt.aov.r1 <- aov_ez(id = "SID", dv = "RT", within = "Repetition",
data = filter(sP3, Familiarity == "Famous"))
anova(p3.rt.aov.r1, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 23 | 242799.6 | 9.8496 | 0.2998 | 0.0046 |
The effect of item repetition was significant in the famous condition.
p3.rt.aov.r2 <- aov_ez(id = "SID", dv = "RT", within = "Repetition",
data = filter(sP3, Familiarity == "Non-famous"))
anova(p3.rt.aov.r2, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 23 | 378424.6 | 1.0624 | 0.0442 | 0.3134 |
The effect of item repetition was not significant in the non-famous condition.
3.3.2 GLMM
To supplement conventional ANOVAs, we performed GLMMs on source memory RT. We built the full model (rt.full) that assumes an inverse Gaussian distribution and a linear relationship (identity link function) between the predictors and RT (Lo & Andrews, 2015). The model included two fixed effects (pre-experimental stimulus familiarity and item repetition) as well as their interaction. The model also included maximal random effects structure (Barr, Levy, Scheepers, & Tily, 2013): both by-participant and by-item random intercepts, and by-participant random slopes for item repetition. This approach is expected to properly handle unbalanced data with a small sample size and skewed distribution such as our RT data.2
(nc <- detectCores())
cl <- makeCluster(rep("localhost", nc))
rt.full <- afex::mixed(RT ~ Familiarity*Repetition + (Repetition|SID) + (1|ImgName),
sP3, method = "LRT", cl = cl,
family=inverse.gaussian(link="identity"),
control = glmerControl(optCtrl = list(maxfun = 1e6)))
stopCluster(cl)anova(rt.full) %>% kable()| Df | Chisq | Chi Df | Pr(>Chisq) | |
|---|---|---|---|---|
| Familiarity | 8 | 2.187735 | 1 | 0.1391138 |
| Repetition | 8 | 1.327305 | 1 | 0.2492852 |
| Familiarity:Repetition | 8 | 4.134498 | 1 | 0.0420175 |
The two-way interaction was significant. Neither main effects were significant. In subsequent pairwise comparisons, the effect of item repetition was significant only for famous faces (see below).
emmeans(rt.full, pairwise ~ Repetition | Familiarity, type = "response")$contrasts %>% kable()| contrast | Familiarity | estimate | SE | df | z.ratio | p.value |
|---|---|---|---|---|---|---|
| Repeated - Unrepeated | Famous | 453.38475 | 109.2457 | Inf | 4.1501379 | 0.0000332 |
| Repeated - Unrepeated | Non-famous | -75.94242 | 111.3944 | Inf | -0.6817437 | 0.4954011 |
4 Session Info
sessionInfo()
## R version 3.5.3 (2019-03-11)
## Platform: x86_64-apple-darwin15.6.0 (64-bit)
## Running under: macOS Mojave 10.14.4
##
## Matrix products: default
## BLAS: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRblas.0.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRlapack.dylib
##
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
##
## attached base packages:
## [1] parallel stats graphics grDevices utils datasets methods
## [8] base
##
## other attached packages:
## [1] klippy_0.0.0.9500 patchwork_0.0.1 RVAideMemoire_0.9-73
## [4] ggbeeswarm_0.6.0 ordinal_2019.3-9 emmeans_1.3.3
## [7] afex_0.23-0 lme4_1.1-21 Matrix_1.2-17
## [10] car_3.0-2 carData_3.0-2 knitr_1.22
## [13] forcats_0.4.0 stringr_1.4.0 dplyr_0.8.0.1
## [16] purrr_0.3.2 readr_1.3.1 tidyr_0.8.3
## [19] tibble_2.1.1 ggplot2_3.1.0 tidyverse_1.2.1
## [22] Rmisc_1.5 plyr_1.8.4 lattice_0.20-38
## [25] pacman_0.5.1
##
## loaded via a namespace (and not attached):
## [1] nlme_3.1-137 lubridate_1.7.4 httr_1.4.0
## [4] numDeriv_2016.8-1 tools_3.5.3 backports_1.1.3
## [7] utf8_1.1.4 R6_2.4.0 vipor_0.4.5
## [10] lazyeval_0.2.2 colorspace_1.4-1 withr_2.1.2
## [13] tidyselect_0.2.5 curl_3.3 compiler_3.5.3
## [16] cli_1.1.0 rvest_0.3.2 xml2_1.2.0
## [19] sandwich_2.5-0 labeling_0.3 scales_1.0.0
## [22] mvtnorm_1.0-10 digest_0.6.18 foreign_0.8-71
## [25] minqa_1.2.4 rmarkdown_1.12 rio_0.5.16
## [28] pkgconfig_2.0.2 htmltools_0.3.6 highr_0.8
## [31] rlang_0.3.3 readxl_1.3.1 rstudioapi_0.10
## [34] generics_0.0.2 zoo_1.8-5 jsonlite_1.6
## [37] zip_2.0.1 magrittr_1.5 fansi_0.4.0
## [40] Rcpp_1.0.1 munsell_0.5.0 abind_1.4-5
## [43] ucminf_1.1-4 stringi_1.4.3 multcomp_1.4-10
## [46] yaml_2.2.0 MASS_7.3-51.3 grid_3.5.3
## [49] crayon_1.3.4 haven_2.1.0 splines_3.5.3
## [52] hms_0.4.2 pillar_1.3.1 boot_1.3-20
## [55] estimability_1.3 reshape2_1.4.3 codetools_0.2-16
## [58] glue_1.3.1 evaluate_0.13 data.table_1.12.0
## [61] modelr_0.1.4 nloptr_1.2.1 cellranger_1.1.0
## [64] gtable_0.3.0 assertthat_0.2.1 xfun_0.5
## [67] openxlsx_4.1.0 xtable_1.8-3 broom_0.5.1
## [70] coda_0.19-2 survival_2.44-1 lmerTest_3.1-0
## [73] beeswarm_0.2.3 TH.data_1.0-10One additional participant in the
non-famousface group was excluded due to failing to respond in two thirds of trials in the second phase.↩We tested additional GLMMs on source memory RTs. One model assumed a Gamma distribution and a linear relationship (identity link function) between the predictors and RTs. The other models adopted non-linear transformations of RTs (such as -1000/RT or log(RT)). None of the models, however, converged onto a stable solution.↩