Experiment 4B
Famous vs. non-famous faces (within-participant design)
Hongmi Lee, Kyungmi Kim, Do-Joon Yi
2019-04-02
set.seed(12345) # for reproducibility
options(knitr.kable.NA = '')
# Some packages need to be loaded. We use `pacman` as a package manager, which takes care of the other packages.
if (!require("pacman", quietly = TRUE)) install.packages("pacman")
if (!require("Rmisc", quietly = TRUE)) install.packages("Rmisc") # Never load it directly.
pacman::p_load(tidyverse, knitr, car, afex, emmeans, parallel, ordinal,
ggbeeswarm, RVAideMemoire)
pacman::p_load_gh("thomasp85/patchwork", "RLesur/klippy")
klippy::klippy()1 Item Repetition Phase
Twenty eight participants were exposed to 20 famous faces and 20 non-famous faces (pre-experimental stimulus familiarity as a within-participant factor). Each face was repeated eight times, resulting in 320 trials. For each face, participants made a male/female judgment.
P1 <- read.csv("data/data_FamSM_Exp4B_Face_REP.csv", header = T)
P1$Familiarity = factor(P1$Familiarity, levels=c(1,2), labels=c("Famous","Non-famous"))
glimpse(P1, width=70)
## Observations: 8,960
## Variables: 9
## $ SID <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ Familiarity <fct> Famous, Famous, Non-famous, Non-famous, Non-fam…
## $ RepTime <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ Trial <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …
## $ ImgCat <int> 1, 2, 2, 1, 1, 1, 2, 2, 1, 2, 1, 1, 1, 1, 1, 2,…
## $ Resp <int> 1, 2, 2, 1, 1, 1, 2, 2, 1, 2, 1, 1, 1, 1, 1, 2,…
## $ Corr <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ RT <dbl> 1623.66, 519.65, 519.63, 511.72, 543.61, 503.75…
## $ ImgName <fct> famous_male06.jpg, famous_female10.jpg, unknown…
# 1. SID: participant ID
# 2. Familiarity: pre-experimental familiarity. 1 = famous, 2 = non-famous
# 3. RepTime: number of repetition, 1~8
# 4. Trial: 1~40
# 5. ImgCat: stimulus category. male vs. female
# 6. Resp: male/female judgment, 1 = male, 2 = female, 0 = no response
# 7. Corr: correctness, 1=correct, 0 = incorrect or no response
# 8. RT: reaction times in ms.
# 9. ImgName: name of stimuli
table(P1$Familiarity, P1$SID)
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
## Famous 160 160 160 160 160 160 160 160 160 160 160 160 160 160 160
## Non-famous 160 160 160 160 160 160 160 160 160 160 160 160 160 160 160
##
## 16 17 18 19 20 21 22 23 24 25 26 27 28
## Famous 160 160 160 160 160 160 160 160 160 160 160 160 160
## Non-famous 160 160 160 160 160 160 160 160 160 160 160 160 1601.1 Accuracy
We calculated the mean and s.d. of individual participants’ mean percentage accuracy. Overall accuracy of the male/female judgment was high. The famous condition showed slightly lower mean accuracy than the non-famous condition. In the following plot, red points and error bars represent the means and 95% CIs (error bars are hidden behind the points).
# phase 1, subject-level, long-format
P1slong <- P1 %>% group_by(SID, Familiarity) %>%
summarise(Accuracy = mean(Corr)*100) %>%
ungroup()
# summary table
P1slong %>% group_by(Familiarity) %>%
summarise(M = mean(Accuracy), SD = sd(Accuracy)) %>%
ungroup() %>%
kable()| Familiarity | M | SD |
|---|---|---|
| Famous | 97.85714 | 1.866715 |
| Non-famous | 98.41518 | 1.506949 |
# group level, needed for printing & geom_pointrange
# Rmisc must be called indirectly due to incompatibility between plyr and dplyr.
P1g <- Rmisc::summarySEwithin(data = P1slong, measurevar = "Accuracy",
idvar = "SID", withinvars = "Familiarity")
ggplot(P1slong, aes(x=Familiarity, y=Accuracy)) +
geom_violin(width = 0.5, trim=TRUE) +
ggbeeswarm::geom_quasirandom(color = "blue", size = 3, alpha = 0.2, width = 0.2) +
geom_pointrange(P1g, inherit.aes=FALSE,
mapping=aes(x = Familiarity, y=Accuracy,
ymin = Accuracy - ci, ymax = Accuracy + ci),
colour="darkred", size = 1)+
coord_cartesian(ylim = c(50, 100), clip = "on") +
labs(x = "Pre-experimental Stimulus Familiarity",
y = "Male/Female Judgment \n Accuracy (%)") +
theme_bw(base_size = 18)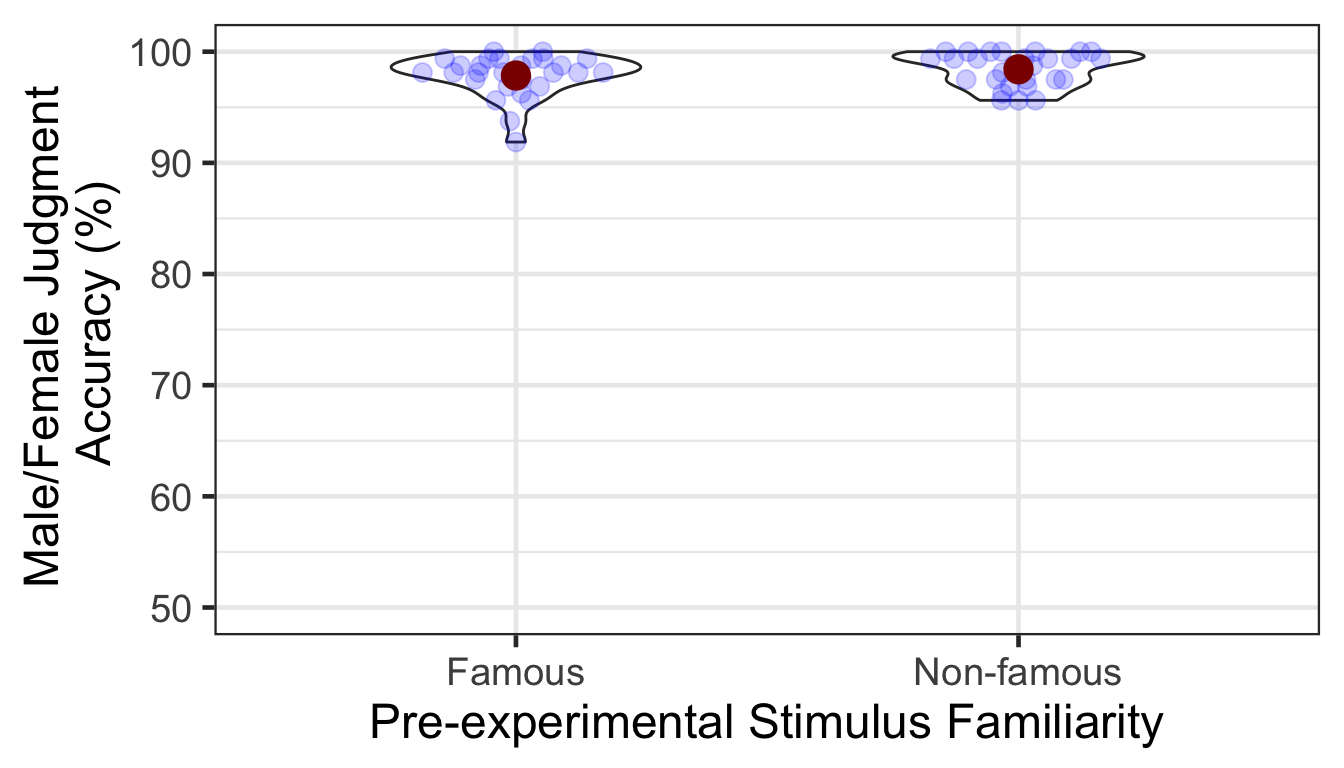
1.1.1 ANOVA
A one-way repeated measures ANOVA revealed that the difference between conditions was marginally significant.
p1.aov <- aov_ez(id = "SID", dv = "Accuracy", data = P1slong, within = "Familiarity")
anova(p1.aov, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Familiarity | 1 | 27 | 1.3649 | 3.1942 | 0.1058 | 0.0851 |
2 Item-Source Association Phase
Participants learned 80 face-location (a quadrant on the screen) associations. They were instructed to pay attention to the location of each face while reporting in which quadrant a face appeared. The design consisted of two within-participant factors: pre-experimental stimulus familiarity (famous or non-famous face) and item repetition (repeated or unrepeated in the first phase).
P2 <- read.csv("data/data_FamSM_Exp4B_Face_SRC.csv", header = T)
P2$Familiarity = factor(P2$Familiarity, levels=c(1,2), labels=c("Famous","Non-famous"))
P2$Repetition = factor(P2$Repetition, levels=c(1,2), labels=c("Repeated","Unrepeated"))
glimpse(P2, width=70)
## Observations: 2,240
## Variables: 9
## $ SID <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ Familiarity <fct> Non-famous, Non-famous, Non-famous, Famous, Non…
## $ Trial <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …
## $ Repetition <fct> Unrepeated, Unrepeated, Unrepeated, Repeated, R…
## $ Loc <int> 3, 1, 3, 4, 3, 1, 4, 4, 3, 3, 2, 4, 3, 2, 3, 3,…
## $ Resp <int> 3, 1, 3, 4, 3, 1, 4, 4, 3, 3, 2, 4, 3, 2, 3, 3,…
## $ Corr <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ RT <dbl> 1096.66, 646.24, 555.80, 609.39, 374.93, 668.45…
## $ ImgName <fct> unknown_female08.jpg, unknown_male07.jpg, unkno…
# 1. SID: participant ID
# 2. Familiarity: pre-experimental familiarity. 1 = famous, 2 = non-famous
# 3. Trial: 1~48
# 4. Repetition: 1 = repetition, 2 = no repetition
# 5. Loc: location (source) of memory item; quadrants, 1~4
# 6. Resp: one of 4 quadrants where a face appeared, 1~4. 0 = no response
# 7. Corr: correctness, 1 = correct, 0 = incorrect or no response
# 8. RT: reaction times in ms.
# 9. ImgName: name of stimuli
table(P2$Familiarity, P2$SID)
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## Famous 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40
## Non-famous 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40
##
## 21 22 23 24 25 26 27 28
## Famous 40 40 40 40 40 40 40 40
## Non-famous 40 40 40 40 40 40 40 40
table(P2$Repetition, P2$SID)
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## Repeated 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40
## Unrepeated 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40
##
## 21 22 23 24 25 26 27 28
## Repeated 40 40 40 40 40 40 40 40
## Unrepeated 40 40 40 40 40 40 40 402.1 Accuracy
We calculated the mean and s.d. of individual participants’ mean percentage accuracy. The accuracy of the localization task was near ceiling, except for one participant (26th) who pressed wrong buttons during the first half of trials.
# phase 2, subject-level, long-format
P2slong <- P2 %>% group_by(SID, Familiarity, Repetition) %>%
summarise(Accuracy = mean(Corr)*100) %>%
ungroup()
# summary table
P2g <- P2slong %>% group_by(Familiarity, Repetition) %>%
summarise(M = mean(Accuracy), SD = sd(Accuracy)) %>%
ungroup()
P2g %>% kable()| Familiarity | Repetition | M | SD |
|---|---|---|---|
| Famous | Repeated | 98.92857 | 5.669467 |
| Famous | Unrepeated | 99.46429 | 2.834734 |
| Non-famous | Repeated | 98.57143 | 5.750546 |
| Non-famous | Unrepeated | 98.39286 | 7.583311 |
# group level, needed for printing & geom_pointrange
# Rmisc must be called indirectly due to incompatibility between plyr and dplyr.
P2g$ci <- Rmisc::summarySEwithin(data = P2slong, measurevar = "Accuracy", idvar = "SID",
withinvars = c("Familiarity", "Repetition"))$ci
P2g$Accuracy <- P2g$M
ggplot(data=P2slong, aes(x=Familiarity, y=Accuracy, fill=Repetition)) +
geom_violin(width = 0.7, trim=TRUE) +
ggbeeswarm::geom_quasirandom(dodge.width = 0.7, color = "blue", size = 3, alpha = 0.2,
show.legend = FALSE) +
# geom_pointrange(data=P2g,
# aes(x = Familiarity, ymin = Accuracy-ci, ymax = Accuracy+ci, color = Repetition),
# position = position_dodge(0.7), color = "darkred", size = 1, show.legend = FALSE) +
coord_cartesian(ylim = c(50, 100), clip = "on") +
labs(x = "Pre-experimental Stimulus Familiarity",
y = "Localization Accuracy (%)",
fill='Item Repetition') +
scale_fill_manual(values=c("#E69F00", "#56B4E9"),
labels=c("Repeated", "Unrepeated")) +
theme_bw(base_size = 18) +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank()) 
2.1.1 ANOVA
Mean percentage accuracy was submitted to a 2x2 repeated measures ANOVA with pre-experimental stimulus familiarity and item repetition as two within-participant factors. No effects were significant.
p2.aov <- aov_ez(id = "SID", dv = "Accuracy", data = P2slong, within = c("Familiarity", "Repetition"))
anova(p2.aov, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Familiarity | 1 | 27 | 5.9524 | 2.4000 | 0.0816 | 0.1330 |
| Repetition | 1 | 27 | 0.8929 | 1.0000 | 0.0357 | 0.3262 |
| Familiarity:Repetition | 1 | 27 | 6.3492 | 0.5625 | 0.0204 | 0.4597 |
3 Source Memory Test Phase
In each trial, participants first indicated in which quadrant a given face appeared during the item-source association phase. Participants then rated how confident they were about their memory judgment. There were 48 trials in total. Both pre-experimental stimulus familiarity and item repetition were manipulated within participants.
P3 <- read.csv("data/data_FamSM_Exp4B_Face_TST.csv", header = T)
P3$Familiarity = factor(P3$Familiarity, levels=c(1,2), labels=c("Famous","Non-famous"))
P3$Repetition = factor(P3$Repetition, levels=c(1,2), labels=c("Repeated","Unrepeated"))
glimpse(P3, width=70)
## Observations: 2,240
## Variables: 10
## $ SID <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1,…
## $ Trial <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, …
## $ Familiarity <fct> Famous, Famous, Non-famous, Non-famous, Famous,…
## $ Repetition <fct> Unrepeated, Unrepeated, Unrepeated, Repeated, R…
## $ AscLoc <int> 3, 2, 3, 3, 1, 1, 3, 3, 4, 4, 4, 1, 4, 1, 4, 4,…
## $ SrcResp <int> 3, 2, 2, 3, 1, 1, 3, 2, 4, 1, 4, 2, 2, 1, 4, 4,…
## $ Corr <int> 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 1, 1,…
## $ RT <dbl> 4298.98, 6481.67, 1785.72, 2810.77, 3664.46, 13…
## $ Confident <int> 4, 4, 4, 4, 4, 4, 2, 4, 4, 1, 4, 1, 4, 1, 4, 4,…
## $ ImgName <fct> famous_male05.jpg, famous_female07.jpg, unknown…
# 1. SID: participant ID
# 2. Familiarity: pre-experimental familiarity. 1 = famous, 2 = non-famous
# 3. Trial: 1~48
# 4. Repetition: 1 = repetition, 2 = no repetition
# 5. AscLoc: location (source) in which the item was presented in Phase 2; quadrants, 1~4
# 6. SrcResp: source response; quadrants, 1~4
# 7. Corr: correctness, 1=correct, 0=incorrect
# 8. RT: reaction times in ms.
# 9. Confident: confidence rating, 1~4
# 10. ImgName: name of stimuli
table(P3$Familiarity, P3$SID)
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## Famous 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40
## Non-famous 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40
##
## 21 22 23 24 25 26 27 28
## Famous 40 40 40 40 40 40 40 40
## Non-famous 40 40 40 40 40 40 40 40
table(P3$Repetition, P3$SID)
##
## 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
## Repeated 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40
## Unrepeated 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40 40
##
## 21 22 23 24 25 26 27 28
## Repeated 40 40 40 40 40 40 40 40
## Unrepeated 40 40 40 40 40 40 40 403.1 Accuracy
We calculated the mean and s.d. of individual participants’ mean percentage accuracy. In the following plot, red points and error bars represent the means and 95% within-participants CIs.
# phase 3, subject-level, long-format
P3ACCslong <- P3 %>% group_by(SID, Familiarity, Repetition) %>%
summarise(Accuracy = mean(Corr)*100) %>%
ungroup()
# summary table
P3ACCg <- P3ACCslong %>% group_by(Familiarity, Repetition) %>%
summarise(M = mean(Accuracy), SD = sd(Accuracy)) %>%
ungroup()
P3ACCg %>% kable()| Familiarity | Repetition | M | SD |
|---|---|---|---|
| Famous | Repeated | 61.25000 | 14.56944 |
| Famous | Unrepeated | 67.85714 | 20.74665 |
| Non-famous | Repeated | 45.89286 | 18.00481 |
| Non-famous | Unrepeated | 40.35714 | 12.90482 |
# marginal means of famous vs. non-famous conditions.
P3ACCslong %>% group_by(Familiarity) %>%
summarise(M = mean(Accuracy), SD = sd(Accuracy)) %>%
ungroup() %>% kable()| Familiarity | M | SD |
|---|---|---|
| Famous | 64.55357 | 18.07250 |
| Non-famous | 43.12500 | 15.77001 |
# marginal means of repeated vs. unrepeated conditions.
P3ACCslong %>% group_by(Repetition) %>%
summarise(M = mean(Accuracy), SD = sd(Accuracy)) %>%
ungroup() %>% kable()| Repetition | M | SD |
|---|---|---|
| Repeated | 53.57143 | 17.98268 |
| Unrepeated | 54.10714 | 22.03524 |
# wide format, needed for geom_segments.
P3ACCswide <- P3ACCslong %>% spread(key = Repetition, value = Accuracy)
# group level, needed for printing & geom_pointrange
# Rmisc must be called indirectly due to incompatibility between plyr and dplyr.
P3ACCg$ci <- Rmisc::summarySEwithin(data = P3ACCslong, measurevar = "Accuracy", idvar = "SID",
withinvars = c("Familiarity", "Repetition"))$ci
P3ACCg$Accuracy <- P3ACCg$M
ggplot(data=P3ACCslong, aes(x=Familiarity, y=Accuracy, fill=Repetition)) +
geom_violin(width = 0.5, trim=TRUE) +
geom_point(position=position_dodge(0.5), color="gray80", size=1.8, show.legend = FALSE) +
geom_segment(data=filter(P3ACCswide, Familiarity=="Famous"), inherit.aes = FALSE,
aes(x=1-.12, y=filter(P3ACCswide, Familiarity=="Famous")$Repeated,
xend=1+.12, yend=filter(P3ACCswide, Familiarity=="Famous")$Unrepeated),
color="gray80") +
geom_segment(data=filter(P3ACCswide, Familiarity=="Non-famous"), inherit.aes = FALSE,
aes(x=2-.12, y=filter(P3ACCswide, Familiarity=="Non-famous")$Repeated,
xend=2+.12, yend=filter(P3ACCswide, Familiarity=="Non-famous")$Unrepeated),
color="gray80") +
geom_pointrange(data=P3ACCg,
aes(x = Familiarity, ymin = Accuracy-ci, ymax = Accuracy+ci, group = Repetition),
position = position_dodge(0.5), color = "darkred", size = 1, show.legend = FALSE) +
scale_fill_manual(values=c("#E69F00", "#56B4E9"),
labels=c("Repeated", "Unrepeated")) +
labs(x = "Pre-experimental Stimulus Familiarity",
y = "Source Memory Accuracy (%)",
fill='Item Repetition') +
coord_cartesian(ylim = c(0, 100), clip = "on") +
theme_bw(base_size = 18) +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank()) 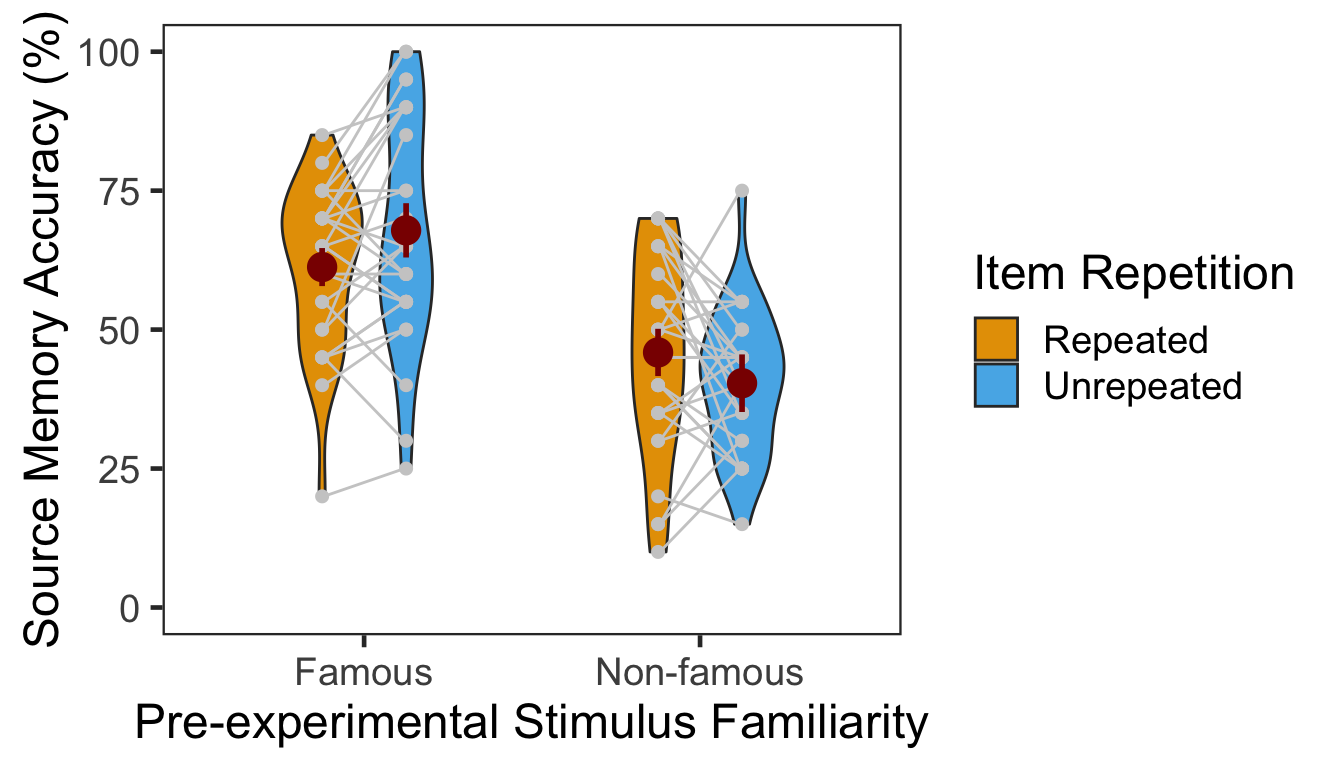
The effect of item repetition was modulated by the pre-experimental familiarity of the items. For famous faces, the locations of unrepeated items were better remembered (novelty benefit). For non-famous faces, the locations of repeated items were better remembered (familiarity benefit). These crossed effects were on top of the general familiarity benefit, in which source memory was more accurate for famous faces than for non-famous faces.
3.1.1 ANOVA
Mean percentage accuracy was submitted to a 2x2 repeated measures ANOVA with pre-experimental stimulus familiarity (famous vs. non-famous) and item repetition (repetition vs. no repetition) as two within-participant factors.
p3.corr.aov <- aov_ez(id = "SID", dv = "Accuracy", data = P3ACCslong, within = c("Familiarity", "Repetition"))
anova(p3.corr.aov, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Familiarity | 1 | 27 | 158.5317 | 81.1014 | 0.7502 | 0.0000 |
| Repetition | 1 | 27 | 104.7950 | 0.0767 | 0.0028 | 0.7840 |
| Familiarity:Repetition | 1 | 27 | 138.1614 | 7.4706 | 0.2167 | 0.0109 |
The main effect of pre-experimental stimulus familiarity and the two-way interaction were both significant. Additionally, we performed two separate one-way repeated-measures ANOVAs as post-hoc analyses. The table below shows the effect of item repetition for famous faces.
ci95 <- P3ACCswide %>% filter(Familiarity=="Famous") %>%
mutate(Diff = Unrepeated - Repeated) %>%
summarise(lower = mean(Diff) - qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()),
upper = mean(Diff) + qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()))
p3.corr.aov.r1 <- aov_ez(id = "SID", dv = "Accuracy", within = "Repetition",
data = filter(P3ACCslong, Familiarity == "Famous"))
anova(p3.corr.aov.r1, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 27 | 98.1978 | 6.2238 | 0.1873 | 0.019 |
In the famous face condition, source memory was more accurate for unrepeated than repeated faces. The 95% CI of difference between the means was [1.17, 12.04]. The table below shows the effect of item repetition for non-famous faces.
ci95 <- P3ACCswide %>% filter(Familiarity=="Non-famous") %>%
mutate(Diff = Repeated - Unrepeated) %>%
summarise(lower = mean(Diff) - qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()),
upper = mean(Diff) + qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()))
p3.corr.aov.r2 <- aov_ez(id = "SID", dv = "Accuracy", within = "Repetition",
data = filter(P3ACCslong, Familiarity == "Non-famous"))
anova(p3.corr.aov.r2, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 27 | 144.7586 | 2.9637 | 0.0989 | 0.0966 |
In the non-famous face condition, source memory was marginally more accurate for repeated than unrepeated faces. The 95% CI of difference between the means was [-1.06, 12.13].
3.1.2 GLMM
To supplement conventional ANOVAs, we performed GLMMs on source memory accuracy. This mixed modeling approach with a binomial link function is expected to properly handle binary data such as source memory responses (i.e., correct or not; Jaeger, 2008).
We built the full model (full1) with two fixed effects (pre-experimental stimulus familiarity and item repetition) and their interaction. The model also included maximal random effects structure (Barr, Levy, Scheepers, & Tily, 2013): both by-participant and by-item random intercepts, and by-participant random slopes for pre-experimental stimulus familiarity, item repetition and their interaction. In case the maximal model does not converge successfully, we built another model (full2) with the maximal random structure but with the correlations among the random terms removed (Singmann, 2018).
To fit the models, we used the mixed() of the afex package (Singmann, Bolker, & Westfall, 2017) which was built on the lmer() of the lme4 package (Bates, Maechler, Bolker, & Walker, 2015). The mixed() assessed the statistical significance of fixed effects by comparing a model with the effect in question against its nested model which lacked the effect in question. P-values of the effects were obtained by likelihood ratio tests (LRT).
(nc <- detectCores())
cl <- makeCluster(rep("localhost", nc))
full1 <- mixed(Corr ~ Familiarity*Repetition + (Familiarity*Repetition|SID) + (1|ImgName),
P3, method = "LRT", cl = cl,
family=binomial(link="logit"),
control = glmerControl(optCtrl = list(maxfun = 1e6)))
full2 <- mixed(Corr ~ Familiarity*Repetition + (Familiarity*Repetition||SID) + (1|ImgName),
P3, method = "LRT", cl = cl,
family=binomial(link="logit"),
control = glmerControl(optCtrl = list(maxfun = 1e6)), expand_re = TRUE)
stopCluster(cl)The table below presents the LRT results of the models full1 and full2.
full.compare <- cbind(afex::nice(full1), afex::nice(full2)[,-c(1,2)])
colnames(full.compare)[c(3,4,5,6)] <- c("full1 Chisq", "p", "full2 Chisq", "p")
full.compare %>% kable()| Effect | df | full1 Chisq | p | full2 Chisq | p |
|---|---|---|---|---|---|
| Familiarity | 1 | 33.44 *** | <.0001 | 36.25 *** | <.0001 |
| Repetition | 1 | 1.05 | .30 | 0.19 | .67 |
| Familiarity:Repetition | 1 | 5.92 * | .01 | 6.62 * | .01 |
The p-values from the two models were highly similar to each other. Post-hoc analysis results are summarized in the table below. The difference between repeated vs. unrepeated faces was significant in the famous condition. However, the difference was not significant in the non-famous condition.
emmeans(full1, pairwise ~ Repetition | Familiarity, type = "response")$contrasts %>% kable()| contrast | Familiarity | odds.ratio | SE | df | z.ratio | p.value |
|---|---|---|---|---|---|---|
| Repeated / Unrepeated | Famous | 0.6652118 | 0.1131780 | Inf | -2.395992 | 0.0165755 |
| Repeated / Unrepeated | Non-famous | 1.2330721 | 0.1771987 | Inf | 1.457907 | 0.1448661 |
3.2 Confidence
The following table presents the mean and s.d. of individual participants’ confidence ratings in each condition. The pattern of confidence ratings was qualitatively identical to that of source memory accuracy; we observed the novelty benefit for famous faces and the familiarity benefit for non-famous faces. In the following plot, red points and error bars represent the means and 95% within-participants CIs.
P3CFslong <- P3 %>% group_by(SID, Familiarity, Repetition) %>%
summarise(Confidence = mean(Confident)) %>%
ungroup()
P3CFg <- P3CFslong %>%
group_by(Familiarity, Repetition) %>%
summarise(M = mean(Confidence), SD = sd(Confidence)) %>%
ungroup()
P3CFg %>% kable()| Familiarity | Repetition | M | SD |
|---|---|---|---|
| Famous | Repeated | 2.894643 | 0.3897623 |
| Famous | Unrepeated | 3.069643 | 0.4619482 |
| Non-famous | Repeated | 2.428571 | 0.4062996 |
| Non-famous | Unrepeated | 1.998214 | 0.4641763 |
# marginal means of famous vs. non-famous conditions.
P3CFslong %>% group_by(Familiarity) %>%
summarise(M = mean(Confidence), SD = sd(Confidence)) %>%
ungroup() %>% kable()| Familiarity | M | SD |
|---|---|---|
| Famous | 2.982143 | 0.4325851 |
| Non-famous | 2.213393 | 0.4836876 |
# marginal means of repeated vs. unrepeated conditions.
P3CFslong %>% group_by(Repetition) %>%
summarise(M = mean(Confidence), SD = sd(Confidence)) %>%
ungroup() %>% kable()| Repetition | M | SD |
|---|---|---|
| Repeated | 2.661607 | 0.4592475 |
| Unrepeated | 2.533929 | 0.7090395 |
# wide format, needed for geom_segments.
P3CFswide <- P3CFslong %>% spread(key = Repetition, value = Confidence)
# group level, needed for printing & geom_pointrange
# Rmisc must be called indirectly due to incompatibility between plyr and dplyr.
P3CFg$ci <- Rmisc::summarySEwithin(data = P3CFslong, measurevar = "Confidence", idvar = "SID",
withinvars = c("Familiarity", "Repetition"))$ci
P3CFg$Confidence <- P3CFg$M
ggplot(data=P3CFslong, aes(x=Familiarity, y=Confidence, fill=Repetition)) +
geom_violin(width = 0.5, trim=TRUE) +
geom_point(position=position_dodge(0.5), color="gray80", size=1.8, show.legend = FALSE) +
geom_segment(data=filter(P3CFswide, Familiarity=="Famous"), inherit.aes = FALSE,
aes(x=1-.12, y=filter(P3CFswide, Familiarity=="Famous")$Repeated,
xend=1+.12, yend=filter(P3CFswide, Familiarity=="Famous")$Unrepeated),
color="gray80") +
geom_segment(data=filter(P3CFswide, Familiarity=="Non-famous"), inherit.aes = FALSE,
aes(x=2-.12, y=filter(P3CFswide, Familiarity=="Non-famous")$Repeated,
xend=2+.12, yend=filter(P3CFswide, Familiarity=="Non-famous")$Unrepeated),
color="gray80") +
geom_pointrange(data=P3CFg,
aes(x = Familiarity, ymin = Confidence-ci, ymax = Confidence+ci, group = Repetition),
position = position_dodge(0.5), color = "darkred", size = 1, show.legend = FALSE) +
scale_fill_manual(values=c("#E69F00", "#56B4E9"),
labels=c("Repeated", "Unrepeated")) +
labs(x = "Pre-experimental Stimulus Familiarity",
y = "Source Memory Confidence",
fill='Item Repetition') +
coord_cartesian(ylim = c(1, 4), clip = "on") +
theme_bw(base_size = 18) +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank())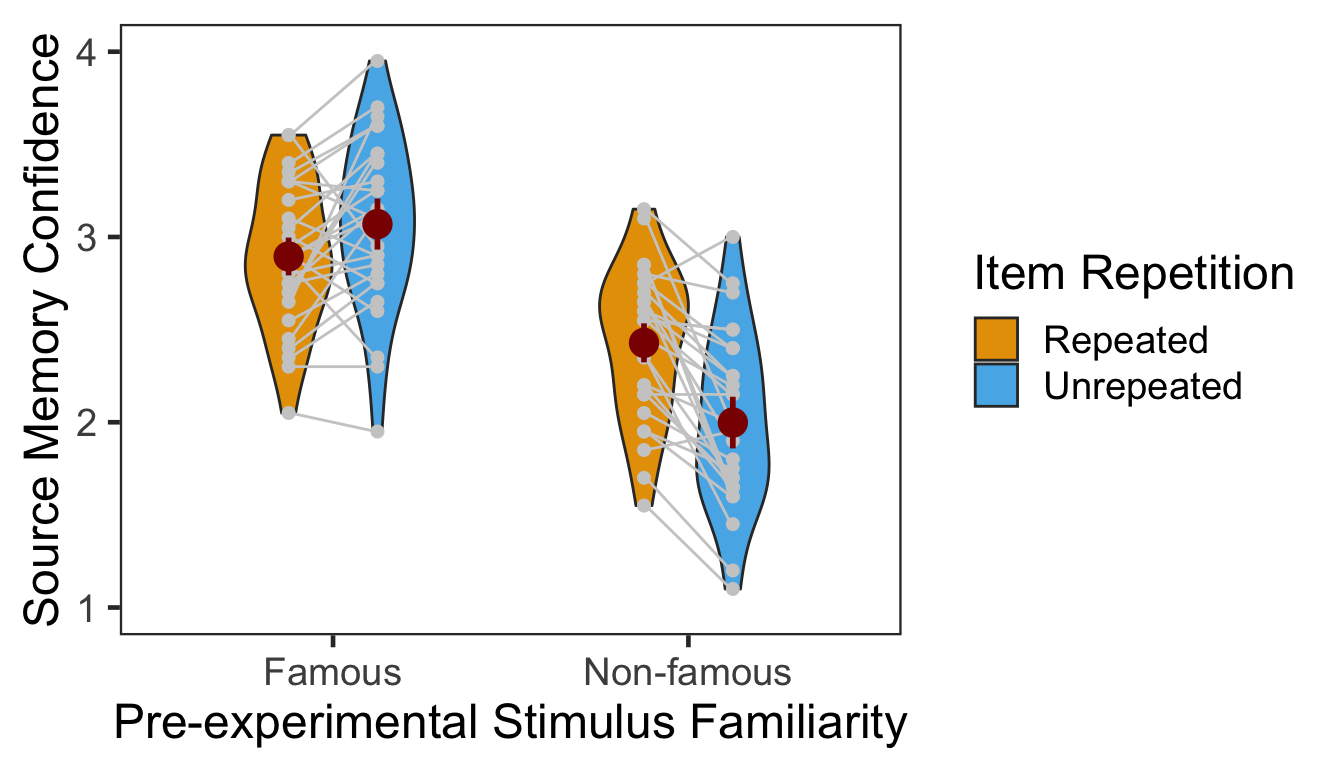
3.2.1 ANOVA
Individuals’ confidence ratings were submitted to a 2x2 repeated measures ANOVA with pre-experimental stimulus familiarity and item repetition as two within-participant factors.
p3.conf.aov <- aov_ez(id = "SID", dv = "Confidence", data = P3CFslong, within = c("Familiarity","Repetition"))
anova(p3.conf.aov, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Familiarity | 1 | 27 | 0.1560 | 106.0405 | 0.7971 | 0.0000 |
| Repetition | 1 | 27 | 0.0552 | 8.2758 | 0.2346 | 0.0078 |
| Familiarity:Repetition | 1 | 27 | 0.0873 | 29.3735 | 0.5211 | 0.0000 |
Confidence ratings were higher in the famous condition than the non-famous condition (the main effect of pre-experimental stimulus familiarity) and higher in the repetition condition than the no repetition condition (the main effect of item repetition). The effect of item repetition was also significantly modulated by the pre-experimental stimulus familiarity. Next we performed two additional one-way repeated-measures ANOVAs as post-hoc analyses. The table below shows the effect of item repetition for famous faces.
ci95 <- P3CFswide %>% filter(Familiarity=="Famous") %>%
mutate(Diff = Unrepeated - Repeated) %>%
summarise(lower = mean(Diff) - qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()),
upper = mean(Diff) + qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()))
p3.conf.aov.r1 <- aov_ez(id = "SID", dv = "Confidence", within = "Repetition",
data = filter(P3CFslong, Familiarity == "Famous"))
anova(p3.conf.aov.r1, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 27 | 0.0684 | 6.2701 | 0.1885 | 0.0186 |
In the famous face condition, confidence ratings were higher for unrepeated than repeated faces. The 95% CI of difference between the means was [0.03, 0.32]. The table below shows the effect of item repetition for non-famous faces.
ci95 <- P3CFswide %>% filter(Familiarity=="Non-famous") %>%
mutate(Diff = Repeated - Unrepeated) %>%
summarise(lower = mean(Diff) - qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()),
upper = mean(Diff) + qt(0.975,df=n()-1)*sd(Diff)/sqrt(n()))
p3.conf.aov.r2 <- aov_ez(id = "SID", dv = "Confidence", within = "Repetition",
data = filter(P3CFslong, Familiarity == "Non-famous"))
anova(p3.conf.aov.r2, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 27 | 0.0741 | 34.9893 | 0.5644 | 0 |
In the non-famous face condition, confidence ratings were higher for repeated than unrepeated faces. The 95% CI of difference between the means was [0.28, 0.58].
3.2.2 CLMM
The responses from a Likert-type scale are ordinal. Especially for the rating items with numerical response formats containing four or fewer categories, it is recommended to use categorical data analysis approaches, rather than treating the responses as continuous data (Harpe, 2015).
Here we employed the cumulative link mixed modeling using the clmm() of the package ordinal (Christensen, submitted). The model specification of fixed and random effects was the same as the mixed() above. To determine the statistical significance, the likelihood ratio tests (LRT) compared models with or without the fixed effect of interest.
P3R <- P3
P3R$Confident = factor(P3R$Confident, ordered = TRUE)
P3R$SID = factor(P3R$SID)
cm.full <- clmm(Confident ~ Familiarity*Repetition + (Familiarity*Repetition|SID) + (1|ImgName), data=P3R)
cm.red1 <- clmm(Confident ~ Familiarity+Repetition + (Familiarity*Repetition|SID) + (1|ImgName), data=P3R)
cm.red2 <- clmm(Confident ~ Repetition+(Familiarity*Repetition|SID) + (1|ImgName), data=P3R)
cm.red3 <- clmm(Confident ~ 1 + (Familiarity*Repetition|SID) + (1|ImgName), data=P3R) cm.comp <- anova(cm.full, cm.red1, cm.red2, cm.red3)
data.frame(Effect = c("Familiarity", "Repetition", "Familiarity:Repetition"),
df = 1, Chisq = cm.comp$LR.stat[2:4], p = cm.comp$`Pr(>Chisq)`[2:4]) %>% kable()| Effect | df | Chisq | p |
|---|---|---|---|
| Familiarity | 1 | 0.7296378 | 0.3930006 |
| Repetition | 1 | 18.9457471 | 0.0000134 |
| Familiarity:Repetition | 1 | 22.5622823 | 0.0000020 |
The LRT revealed that the main effect of item repetition and the two-way interaction were both significant. Next we performed pairwise comparisons as post-hoc analyses. As shown in the following table, the results of the pairwise comparisons were consistent with those from the ANOVA approach.
emmeans(cm.full, pairwise ~ Repetition | Familiarity)$contrasts %>% kable()| contrast | Familiarity | estimate | SE | df | z.ratio | p.value |
|---|---|---|---|---|---|---|
| Repeated - Unrepeated | Famous | -0.4571763 | 0.1395512 | Inf | -3.276046 | 0.0010527 |
| Repeated - Unrepeated | Non-famous | 0.8613610 | 0.1460459 | Inf | 5.897879 | 0.0000000 |
Below is the plot of estimated marginal means, which were extracted from the fitted CLMM. The estimated distribution of confidence ratings shows the interaction between item repetition and pre-experimental stimulus familiarity.
temp <- emmeans(cm.full,~Familiarity:Repetition|cut, mode="linear.predictor")
temp <- rating.emmeans(temp)
temp <- temp %>% unite(Condition, c("Familiarity", "Repetition"))
ggplot(data = temp, aes(x = Rating, y = Prob, group = Condition)) +
geom_line(aes(color = Condition), size = 1.2) +
geom_point(aes(shape = Condition, color = Condition), size = 4, fill = "white", stroke = 1.2) +
scale_color_manual(values=c("#E69F00", "#E69F00", "#56B4E9", "#56B4E9")) +
scale_shape_manual(name="Condition", values=c(21,24,21,24)) +
labs(y = "Response Probability", x = "Rating") +
expand_limits(y=0) +
scale_y_continuous(limits = c(0, 0.6)) +
scale_x_discrete(labels = c("1" = "1(Guessed)","4"="4(Sure)")) +
theme_minimal() +
theme(text = element_text(size=18))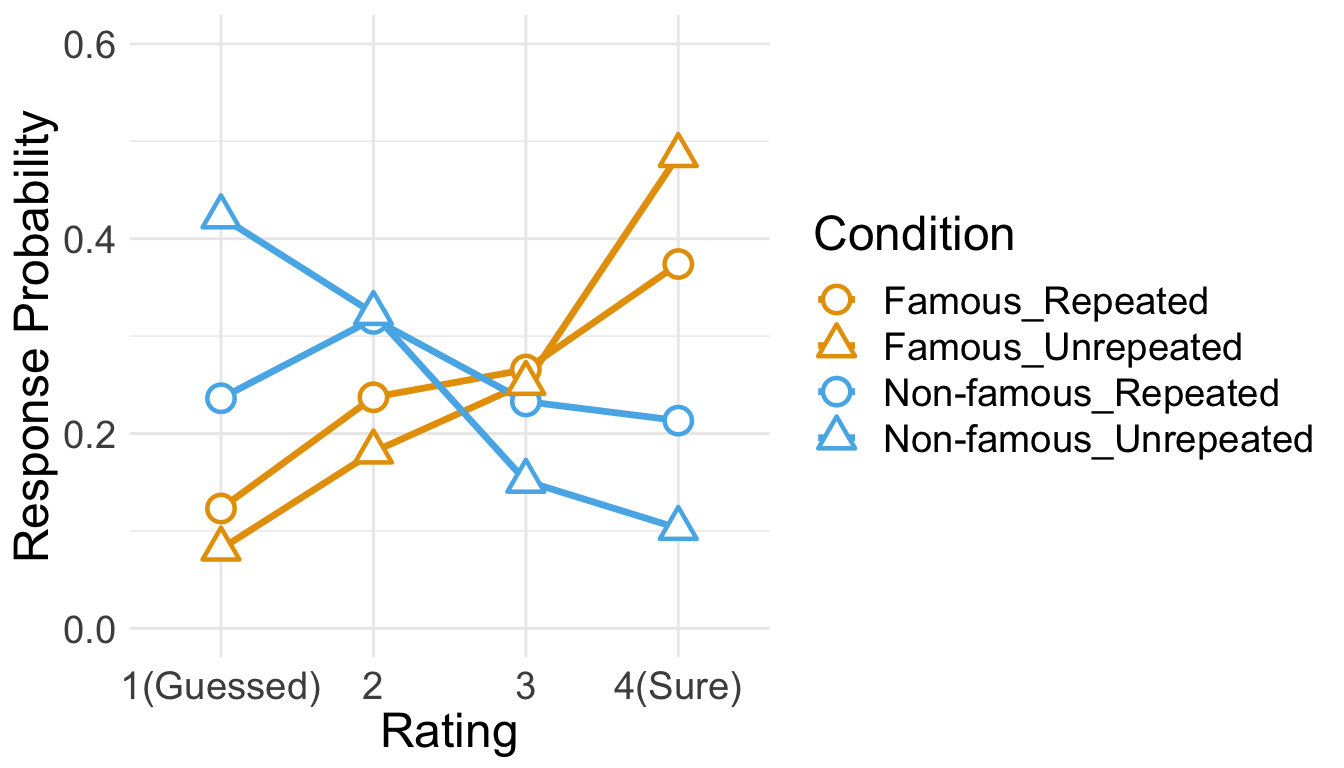
3.3 RT
Only RTs from correct trials were analyzed. Before analysis, we first removed RTs either shorter than 200ms or longer than 10s. Then, from the RT distribution of each condition, RTs beyond 3 s.d. from the mean were additionally removed.
cP3 <- P3 %>% filter(Corr==1)
sP3 <- cP3 %>% filter(RT > 200 & RT < 10000) %>%
group_by(SID) %>%
nest() %>%
mutate(lbound = map(data, ~mean(.$RT)-3*sd(.$RT)),
ubound = map(data, ~mean(.$RT)+3*sd(.$RT))) %>%
unnest(lbound, ubound) %>%
unnest(data) %>%
ungroup() %>%
mutate(Outlier = (RT < lbound)|(RT > ubound)) %>%
filter(Outlier == FALSE) %>%
select(SID, Familiarity, Repetition, RT, ImgName)
100 - 100*nrow(sP3)/nrow(cP3)
## [1] 3.150912This trimming procedure removed 3.15% of correct RTs.
Since the overall source memory accuracy was not high, only small numbers of correct trials were available after trimming. The following table summarizes the numbers of RTs submitted to subsequent analyses. No participant had more than 20 trials per condition. For non-famous faces, half of the participants had less than 10 valid trials per condition.
sP3 %>% group_by(SID, Familiarity, Repetition) %>%
summarise(NumTrial = length(RT)) %>%
ungroup() %>%
group_by(Familiarity, Repetition) %>%
summarise(Mean = mean(NumTrial),
Median = median(NumTrial),
Min = min(NumTrial),
Max = max(NumTrial)) %>%
ungroup %>%
kable()| Familiarity | Repetition | Mean | Median | Min | Max |
|---|---|---|---|---|---|
| Famous | Repeated | 11.678571 | 12.5 | 4 | 16 |
| Famous | Unrepeated | 13.357143 | 13.0 | 5 | 20 |
| Non-famous | Repeated | 8.928571 | 9.0 | 2 | 14 |
| Non-famous | Unrepeated | 7.750000 | 7.5 | 3 | 15 |
den1 <- ggplot(cP3, aes(x=RT)) +
geom_density() +
theme_bw(base_size = 18) +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank())
den2 <- ggplot(sP3, aes(x=RT)) +
geom_density() +
theme_bw(base_size = 18) +
labs(x = "Trimmed RT") +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank())
den1 + den2
The overall RT distribution was highly skewed even after trimming. Given limited numbers of RTs and its skewed distribution, any results from the current RT analyses should be interpreted with caution and preferably corroborated with other measures.
We calculated the mean and s.d. of individual participants’ mean RTs. The overall pattern of RTs across the conditions was consistent with that of source memory accuracy and confidence ratings. In the following plot, red points and error bars represent the means and 95% within-participants CIs.
P3RTslong <- sP3 %>% group_by(SID, Familiarity, Repetition) %>%
summarise(RT = mean(RT)) %>%
ungroup()
P3RTg <- P3RTslong %>% group_by(Familiarity, Repetition) %>%
summarise(M = mean(RT), SD = sd(RT)) %>%
ungroup()
P3RTg %>% kable()| Familiarity | Repetition | M | SD |
|---|---|---|---|
| Famous | Repeated | 2578.924 | 843.4831 |
| Famous | Unrepeated | 2211.463 | 700.1426 |
| Non-famous | Repeated | 2544.358 | 860.1262 |
| Non-famous | Unrepeated | 2724.987 | 1027.0407 |
# wide format, needed for geom_segments.
P3RTswide <- P3RTslong %>% spread(key = Repetition, value = RT)
# group level, needed for printing & geom_pointrange
# Rmisc must be called indirectly due to incompatibility between plyr and dplyr.
P3RTg$ci <- Rmisc::summarySEwithin(data = P3RTslong, measurevar = "RT", idvar = "SID",
withinvars = c("Familiarity", "Repetition"))$ci
P3RTg$RT <- P3RTg$M
ggplot(data=P3RTslong, aes(x=Familiarity, y=RT, fill=Repetition)) +
geom_violin(width = 0.5, trim=TRUE) +
geom_point(position=position_dodge(0.5), color="gray80", size=1.8, show.legend = FALSE) +
geom_segment(data=filter(P3RTswide, Familiarity=="Famous"), inherit.aes = FALSE,
aes(x=1-.12, y=filter(P3RTswide, Familiarity=="Famous")$Repeated,
xend=1+.12, yend=filter(P3RTswide, Familiarity=="Famous")$Unrepeated),
color="gray80") +
geom_segment(data=filter(P3RTswide, Familiarity=="Non-famous"), inherit.aes = FALSE,
aes(x=2-.12, y=filter(P3RTswide, Familiarity=="Non-famous")$Repeated,
xend=2+.12, yend=filter(P3RTswide, Familiarity=="Non-famous")$Unrepeated),
color="gray80") +
geom_pointrange(data=P3RTg,
aes(x = Familiarity, ymin = RT-ci, ymax = RT+ci, group = Repetition),
position = position_dodge(0.5), color = "darkred", size = 1, show.legend = FALSE) +
scale_fill_manual(values=c("#E69F00", "#56B4E9"),
labels=c("Repeated", "Unrepeated")) +
labs(x = "Pre-experimental Stimulus Familiarity",
y = "Response Times (ms)",
fill='Item Repetition') +
theme_bw(base_size = 18) +
theme(panel.grid.major = element_blank(),
panel.grid.minor = element_blank())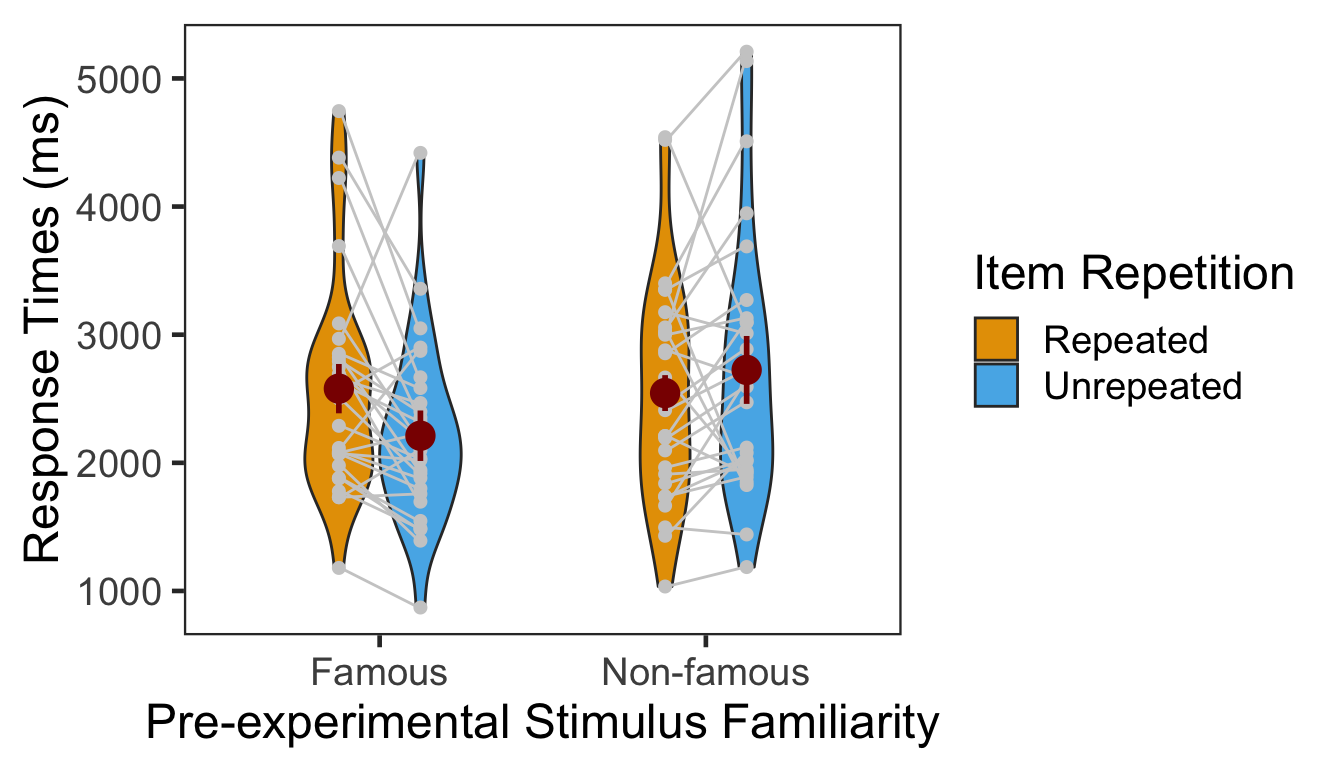
3.3.1 ANOVA
Individuals’ mean RTs were submitted to a 2x2 repeated measures ANOVA with pre-experimental stimulus familiarity and item repetition as two within-participant factors.1
p3.rt.aov <- aov_ez(id = "SID", dv = "RT", data = sP3, within = c("Familiarity", "Repetition"))
anova(p3.rt.aov, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Familiarity | 1 | 27 | 314701.7 | 5.1026 | 0.1589 | 0.0322 |
| Repetition | 1 | 27 | 189067.3 | 1.2924 | 0.0457 | 0.2656 |
| Familiarity:Repetition | 1 | 27 | 322569.0 | 6.5190 | 0.1945 | 0.0166 |
The main effect of pre-experimental stimulus familiarity and the two-way interaction were both significant. The main effect of item repetition was only marginally significant. We then performed two one-way repeated-measures ANOVAs as post-hoc analyses. The first table below presents the effect of item repetition for famous faces, and the second table presents the same effect for non-famous faces.
p3.rt.aov.r1 <- aov_ez(id = "SID", dv = "RT", within = "Repetition",
data = filter(sP3, Familiarity == "Famous"))
anova(p3.rt.aov.r1, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 27 | 220981.5 | 8.5545 | 0.2406 | 0.0069 |
The effect of item repetition was significant in the famous condition.
p3.rt.aov.r2 <- aov_ez(id = "SID", dv = "RT", within = "Repetition",
data = filter(sP3, Familiarity == "Non-famous"))
anova(p3.rt.aov.r2, es = "pes") %>% kable(digits = 4)| num Df | den Df | MSE | F | pes | Pr(>F) | |
|---|---|---|---|---|---|---|
| Repetition | 1 | 27 | 290654.8 | 1.5715 | 0.055 | 0.2207 |
The effect of item repetition was not significant in the non-famous condition.
4 Session Info
sessionInfo()
## R version 3.5.3 (2019-03-11)
## Platform: x86_64-apple-darwin15.6.0 (64-bit)
## Running under: macOS Mojave 10.14.4
##
## Matrix products: default
## BLAS: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRblas.0.dylib
## LAPACK: /Library/Frameworks/R.framework/Versions/3.5/Resources/lib/libRlapack.dylib
##
## locale:
## [1] en_US.UTF-8/en_US.UTF-8/en_US.UTF-8/C/en_US.UTF-8/en_US.UTF-8
##
## attached base packages:
## [1] parallel stats graphics grDevices utils datasets methods
## [8] base
##
## other attached packages:
## [1] klippy_0.0.0.9500 patchwork_0.0.1 RVAideMemoire_0.9-73
## [4] ggbeeswarm_0.6.0 ordinal_2019.3-9 emmeans_1.3.3
## [7] afex_0.23-0 lme4_1.1-21 Matrix_1.2-17
## [10] car_3.0-2 carData_3.0-2 knitr_1.22
## [13] forcats_0.4.0 stringr_1.4.0 dplyr_0.8.0.1
## [16] purrr_0.3.2 readr_1.3.1 tidyr_0.8.3
## [19] tibble_2.1.1 ggplot2_3.1.0 tidyverse_1.2.1
## [22] Rmisc_1.5 plyr_1.8.4 lattice_0.20-38
## [25] pacman_0.5.1
##
## loaded via a namespace (and not attached):
## [1] nlme_3.1-137 lubridate_1.7.4 httr_1.4.0
## [4] numDeriv_2016.8-1 tools_3.5.3 backports_1.1.3
## [7] utf8_1.1.4 R6_2.4.0 vipor_0.4.5
## [10] lazyeval_0.2.2 colorspace_1.4-1 withr_2.1.2
## [13] tidyselect_0.2.5 curl_3.3 compiler_3.5.3
## [16] cli_1.1.0 rvest_0.3.2 xml2_1.2.0
## [19] sandwich_2.5-0 labeling_0.3 scales_1.0.0
## [22] mvtnorm_1.0-10 digest_0.6.18 foreign_0.8-71
## [25] minqa_1.2.4 rmarkdown_1.12 rio_0.5.16
## [28] pkgconfig_2.0.2 htmltools_0.3.6 highr_0.8
## [31] rlang_0.3.3 readxl_1.3.1 rstudioapi_0.10
## [34] generics_0.0.2 zoo_1.8-5 jsonlite_1.6
## [37] zip_2.0.1 magrittr_1.5 fansi_0.4.0
## [40] Rcpp_1.0.1 munsell_0.5.0 abind_1.4-5
## [43] ucminf_1.1-4 stringi_1.4.3 multcomp_1.4-10
## [46] yaml_2.2.0 MASS_7.3-51.3 grid_3.5.3
## [49] crayon_1.3.4 haven_2.1.0 splines_3.5.3
## [52] hms_0.4.2 pillar_1.3.1 boot_1.3-20
## [55] estimability_1.3 reshape2_1.4.3 codetools_0.2-16
## [58] glue_1.3.1 evaluate_0.13 data.table_1.12.0
## [61] modelr_0.1.4 nloptr_1.2.1 cellranger_1.1.0
## [64] gtable_0.3.0 assertthat_0.2.1 xfun_0.5
## [67] openxlsx_4.1.0 xtable_1.8-3 broom_0.5.1
## [70] coda_0.19-2 survival_2.44-1 lmerTest_3.1-0
## [73] beeswarm_0.2.3 TH.data_1.0-10We additionally tested several GLMMs on source memory RTs since GLMMs with relevant link functions are expected to properly handle unbalanced data with a small sample size and skewed distribution such as our RT data (Lo & Andrews, 2015). Some models adopted non-linear transformations of RTs (such as -1000/RT or log(RT)) and others assumed an inverse Gaussian or Gamma distribution and a linear relationship (identity link function) between the predictors and RTs. None of the models, however, converged onto a stable solution.↩